理解麦克斯韦方程组

前言

麦克斯韦方程组 被评为最美公式之一！区区几个方程就一统了电磁学领域，仅凭这一点，有几个对手敢与之一战？

面对纷纷扰扰的电磁学实验结论以及百家争鸣般的各种解释，麦克斯韦是如何一步步透过现象看到本质的呢？各位准备好自己的膝盖，一起来看看麦克斯韦的封神之路吧。

库仑定律

事情还得从牛顿开始说起，至从这哥们提出了万有引力定律 是如此的深入人心。

当各种电现象不断展现在人们面前时，人们发现电与电之间也存在类似引力一样的相互吸引现象。换做是你处于那个时代，你是不是也会有理由猜测电与电之间的相互作用同样满足平方反比定律呢？

于是，怎样验证这个猜想就是当时亟待解决的问题。

高中物理课本里已经用了较大篇幅去介绍库仑扭称实验，结果皆大欢喜，平方反比的猜测是正确的。

其实关于这个猜想的实验验证一直到现代都还在做，最新的实验结果已经在及其高的精度下确认了猜想的正确性！因为这个猜想要是错了的话，整个物理大厦估计又要推倒重建了。

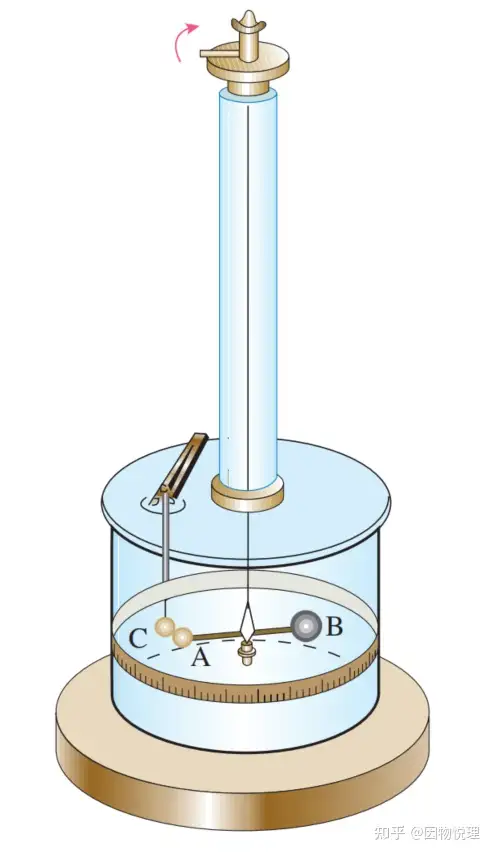
库仑的扭称实验装置

于是乎，大名鼎鼎的库仑定律就横空出现了：真空中两个静止点电荷之间的作用力，其大小与两个点电荷的电量成正比、与两者连线的距离平方成反比，方向沿着两点的连线。即：

$\\F = \frac{{k{q_1}{q_2}}}{{{r^2}}} \\$

式子里的kkk为 比例系数 ，其结果取决于所使用的单位制。

在电磁学的发展历程里，出现过好几种单位制，这个系列的文章里会统一使用 国际单位制 。

所以比例系数为

$\\k = \frac{1}{{4\pi {\varepsilon _0}}}\\$

常数${\varepsilon _0}$被称为真空环境里的 介电常数 ，其结果为：

$\\{\varepsilon _0} \approx 8.854 \times {10^{ - 12}}F/m\\$

至于数值怎么来的，这可不是本篇文章的关注点，略。

另外，为了在定律的结果里体现出作用力的方向，库仑定律的 矢量 （向量与矢量本就是同一个意思，只是在物理领域里习惯称为矢量）表达式为：$\\{\mathbf{F}} = \frac{1}{{4\pi {\varepsilon _0}}}\frac{{{q_1}{q_2}}}{{{r^2}}} \cdot {\mathbf{r}}\\$

式子里的${\mathbf{r}}$是沿着两点连线的单位矢量（方向沿正方向、长度为1）。

库仑定律虽然正确给出了电荷间的相互作用规律，但是没能回答传递这个相互作用的介质是什么。由于电荷不需要接触就能产生相互作用，即使它们身处真空环境也能如此，这和有质量的物体之间能产生引力一样。

于是万有引力定律和库仑定律一拍即合给超距作用观点站队：即认为这类不需要接触就能产生的力不需要任何媒介，而且力不需要时间就能从一个物体作用到相隔一定距离的另一个物体上。

虽然这种观点略带一些神秘色彩，但是奈何两个定律管用，再加上质疑者也没能给出合理的解释，所以这个观点一度占据着统治地位。嗨，前人造坑后人填，把争议交给时间，静待高手出现。

当时光来到法拉第的时代，电磁学迎来了井喷式地发展。提起法拉第，大家首先想到的就是他发现了电磁感应现象，不过大神的贡献远不止这些！他对电介质的研究促使他形成了“力线”的观点，这就是场的初步思想。

于是法拉第旗帜鲜明地反对超距作用的观点，并且给出了强有力的解释，这里面的细节都够详细写上很多文字了，此处就省略一万字吧。场的想法后来被麦克斯韦发扬光大，这才有了最美公式的诞生。

现在让咱们跨越历史，用场的观点来回望电磁学的发展吧。场（这里指电磁场）被认定为电荷间产生相互作用的媒介（与上篇文章)不同，那里的场就是场所的意思），当一个电荷存在时，由它激发的电场就会与其形影不离。

虽然电场看不见也摸不着，但是这个媒介的特点就是对放入其中的另一个电荷有力的作用！

既然引入一个新电荷就能让原有电荷的电场“现原形”，因为新电荷会受到某个方向、一定大小的力，于是咱们顺水推舟，就用新电荷的这些外在表现来反映原有电场的特征吧。

这便有了高中生非常熟悉的一个概念：电场强度 ${\mathbf{E}}$。其定义的思路很朴实——这个空间到底有没有电场，我拿一个检验电荷来检验一下不就清楚了么？

这个检验电荷要是受到力的作用就说明此处有电场，然后用受到的力${\mathbf{F}}$除以自身的电荷量q，比值就能反应出空间该位置处的电场强弱，即
$\\{\mathbf{E}} = \frac{{\mathbf{F}}}{q}\\$

假如你用的是带正电的检验电荷，则空间该位置的电场强度方向就与此检验电荷在该处的受力方向相同。

咱们把激发出待研究电场的电荷称为场源电荷，其电荷量用$Q$表示。最简单的场源电荷就是点电荷啦，利用库仑定律算出场源点电荷与检验电荷之间的静电力，再按照电场强度的定义就能得到点电荷所激发的电场强度为：
$\\{\mathbf{E}} = \frac{1}{{4\pi {\varepsilon _0}}}\frac{Q}{{{r^2}}} \cdot {\mathbf{r}}\\$

悄悄告诉你，库仑定律或者点电荷的电场强度可以说是整个静电学的火种！

因为任何带电物体都可以看成是点电荷的集合，既然拿捏住了单个点电荷的电场强度的特点，那么所有点电荷单独产生的电场叠加之后就是这个带电物体实际激发的电场了。这不就是一个数学问题了么？微积分拿出来用就完事了。

不过理论上的事还得看看实际是否可行，微积分虽好，但是过于复杂的计算也是很困难滴。所以在定律的指导下推出一些实用性更强的定理就显得很重要了。

静电场的 高斯定理 和环路定理

场虽然看不见摸不着，不过法拉第创造的“力线”工具（也就是场线）却能很形象地描绘场的特点。

对于点电荷来说，电场线是从自身发散的一系列射线。如果以点电荷为圆心，以某一距离rrr为半径弄一个球面包住这个点电荷，则电场线与球面处处垂直。

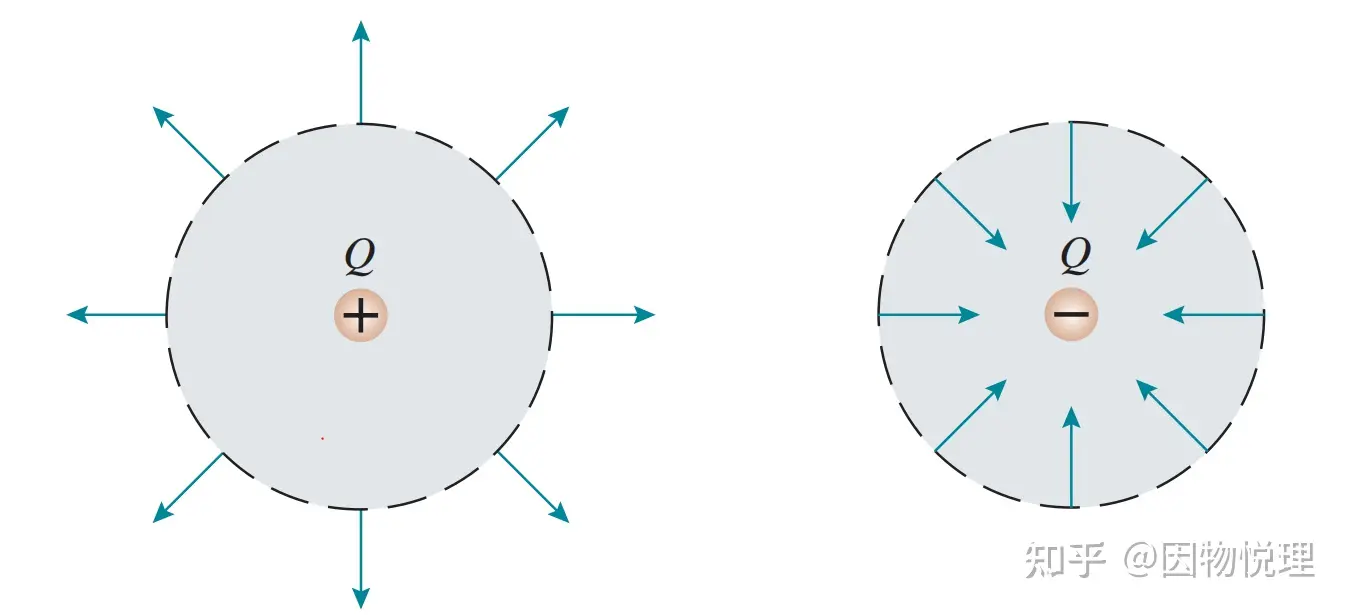
点电荷的电场线

这个图是不是会让你想起通量的例子呢？点电荷的场强特点是同一球面上的各处强度大小相等，且各处的场强方向与球面的法线方向共线，所以对于这个闭合球面求通量的结果就很简单了，有：

$\mathop{{\oiint}}\limits_S {{\mathbf{E}} \cdot d{\mathbf{S}}} = \frac{1}{{4\pi {\varepsilon _0}}}\frac{Q}{{{r^2}}} \cdot 4\pi {r^2} = \frac{Q}{{{\varepsilon _0}}}\\$
可喜的是，数学会给你严格保证：不论是点电荷还是具有一定形状的带电体，当用一个闭合曲面包住它时，其激发的静电场穿过这个闭合曲面的通量始终为一个定值——即为刚才用特例计算的结果。

这便是大名鼎鼎的静电场的高斯定理：

$\mathop{{ \oiint}}\limits_S {{\mathbf{E}} \cdot d{\mathbf{S}}} = \frac{Q}{{{\varepsilon _0}}}\\$

式子里的Q为这个带电体所带的电荷量。

看着眼熟吧？这就是麦克斯韦方程组的第一个方程！毕竟麦神在统一 电磁场理论 的过程里，发现可以用矢量场的通量来描述矢量场的特点。喂，静电场的高斯定理被我收购了哈。

再来看另外一个结论。鉴于点电荷的电场强度特点，你会发现在静电场里移动检验电荷时，无论检验电荷沿着什么路径移动，在这个过程里，静电力做功的结果只与初末位置有关，与移动的路径没有关系。

微积分知识稍微用一下就能得到如下结论：

$\int_{{r_1}}^{{r_2}} {q{\mathbf{E}} \cdot d{\mathbf{r}}} = \frac{{qQ}}{{4\pi {\varepsilon _0}}}\left( {\frac{1}{{{r_1}}} - \frac{1}{{{r_2}}}} \right) \\$

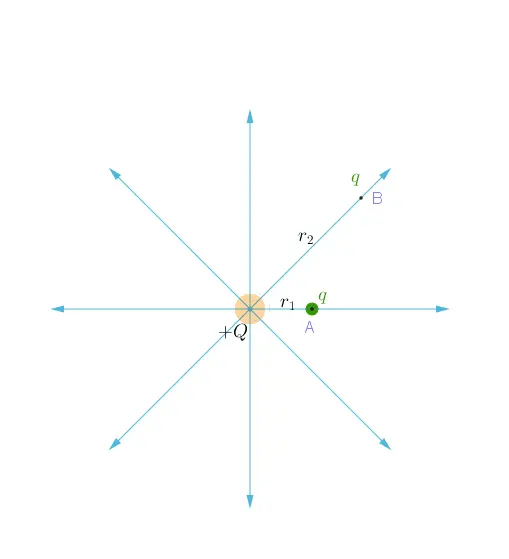
静电力做功的特点——与电荷运动的路径无关

按照这个特点，如果这段路径的起点和终点重合，那么上面这个积分的结果就为零。

也就是说把检验电荷在点电荷激发的静电场里沿着任意一条闭合曲线移动一周，检验电荷受到的电场力做功为零，记成

$\oint\limits_l {q{\mathbf{E}} \cdot d{\mathbf{l}} = 0} \\$把检验电荷的电荷量约掉，则有

$\oint\limits_l {{\mathbf{E}} \cdot d{\mathbf{l}} = 0} \\$

数学同样可以向你担保：一般带电体所激发的静电场也有同样的结论，这便是静电场的环路定理。麦神说矢量场的环量也是描述矢量场特点必不可少的物理量，所以静电场的环路定理也就不客气地笑纳了。

等等，静电场的环路定理好像和麦克斯韦方程组里的方程有点不一样！好吧，被你发现了！稍安勿躁，先搁置一下。

毕奥-萨伐尔定律

现在再把目光放到磁现象身上。人们很早就发现磁现象和电现象有很多相似的地方，只是苦于找不到证据实锤它们在拍拖。当时间来到1820年，随着划时代的奥斯特实验 现象被偶然发现，电磁学迎来了自己的春天。

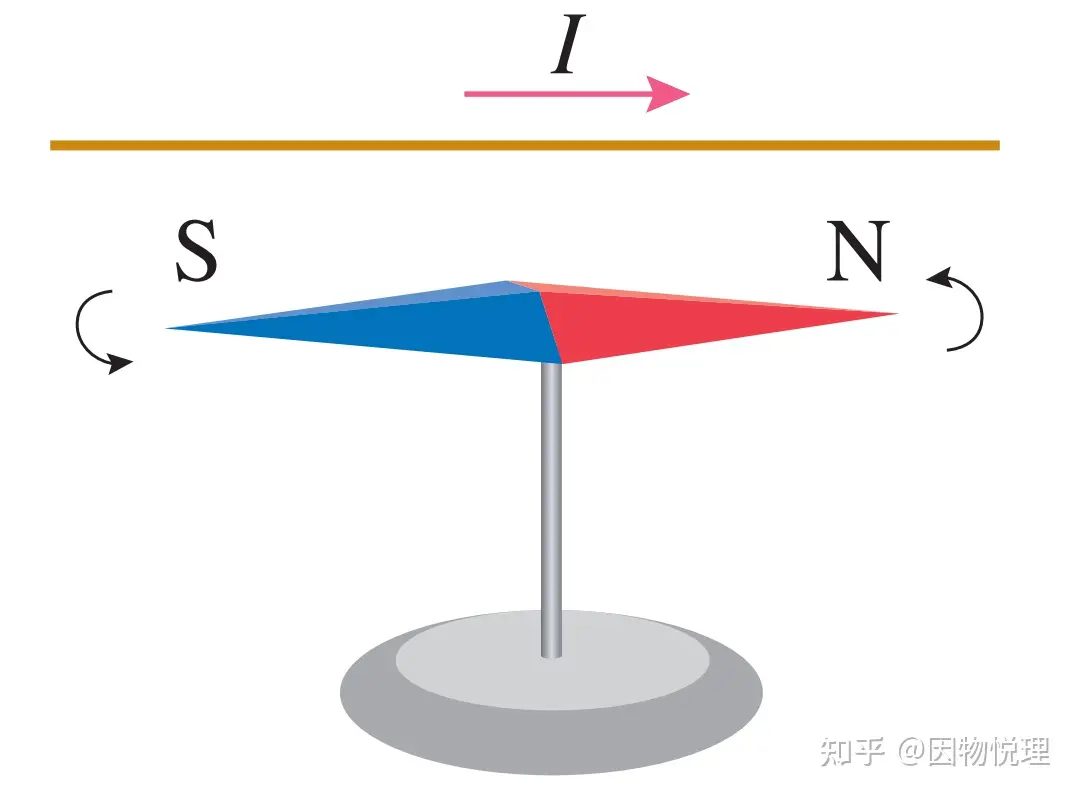
小磁针微微一转，电和磁紧紧地缠绕在了一起

由于 电流磁效应 的发现，短短几个月内硕果累累！毕奥与萨伐尔认为小磁针之所以会发生偏转，是因为电流对小磁针产生了作用力，于是很快通过实验确定了电流对磁极所产生的作用力的定量规律，毫不意外的是，此力大小也是满足平方反比规律的：

$dF = k\frac{{Idl}}{{{r^2}}}\\$

式中的$Idl$称为电流元，你可以理解为是一小段通有电流的导线；$r$为电流元与磁极之间的距离。

考虑到作用力的方向特点——垂直于电流元与磁极的连线方向！所以作用力的矢量表达式应该写成：

$\\d{\mathbf{F}} = k\frac{{Id{\mathbf{l}} \times {\mathbf{r}}}}{{{r^2}}}\\$

顺便提一下，这个作用力的方向特点便是奥斯特把通电导线沿着磁针方向放置时总是无法看到磁针偏转的原因。

同一时期，安培在同样的背景下走得更远一点。他认为磁的作用本质上是电流之间的作用，这不就提出了著名的 安培分子电流假说 么？

磁极有磁性是因为它内部有大量的分子电流，所以磁极在电流作用下发生偏转的根本原因是电流之间的作用导致的。于是他的目光自然就落在了找寻电流之间相互作用的定量规律上。

同样是在很短时间内（不得不说，大佬卷起来也是很拼的），他通过实验确定了两个电流元之间的作用力特点：此力的大小正比于两个电流元的乘积，与电流元的距离平方成反比。

按照下图中标识的记号，作用力的大小可以写成：

$d{F_{12}} = k\frac{{\left( {{I_1}d{l_1}} \right)\left( {{I_2}d{l_2}} \right)}}{{{r^2}}}\\$

考虑到大佬有如此重要的贡献，此力就署上安培的大名吧。

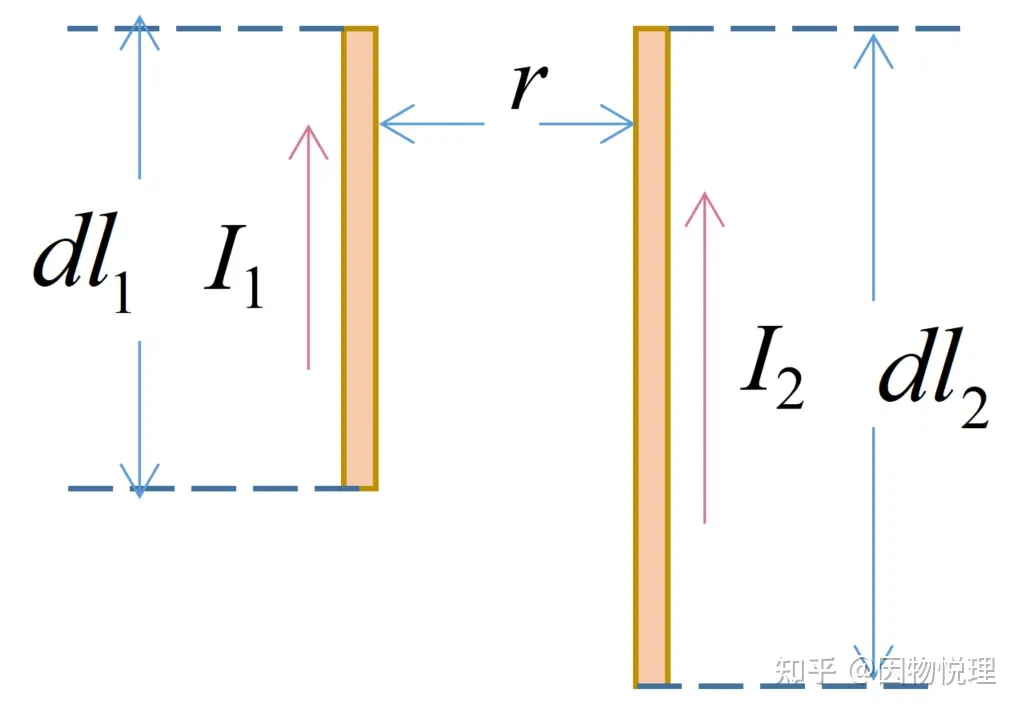
电流元的示意图

如果希望把力的方向特点在 安培力 的表达式里体现出来，则表达式略微有些复杂，你看看就好：

$d{{\mathbf{F}}_{12}} = k\frac{{({I_2}d{{\mathbf{l}}_2}) \times ({I_1}d{{\mathbf{l}}_1} \times {\mathbf{r}})}}{{{r^2}}}\\$

这个矢量式反映了电流元1给电流元2的安培力大小和方向。关于方向的解读，稍后安排。

面对不需要接触就能产生相互作用的两个电流元，并且相互作用也满足平方反比规律，安培倒向了超距作用这个阵营。

这里我们再次打开上帝视角对超距作用说不！电流与电流之间产生相互作用依然是借助场来实现的，这里的场是电流激发的磁场！

既然磁场充当着电流元之间产生作用力的媒介，显然需要一个物理量来描述此媒介的特征，这个光荣的任务就落在了磁感应强度的身上。之所以没叫磁场强度，是因为这个名字早被占坑了。

由于早期磁现象的研究一度类比于库仑定律而提出了磁荷、磁场强度和磁库仑定律，而这些观点也不全都一无是处，所以磁场强度的名称就没有被摘牌。

类比于电场强度的定义，磁感应强度的定义是通过检验电流元所受的安培力给出的。

既然咱们已经得到了电流元1给电流元2的作用力，我们选定电流元1为场源电流元，电流元2为检验电流元，则安培力可以改写成

$d{{\mathbf{F}}_{12}} = ({I_2}d{{\mathbf{l}}_2}) \times d{{\mathbf{B}}_1}\\$

这里的$d{{\mathbf{B}}_1}$就是场源电流元所激发的磁场在检验电流元所处位置的磁感应强度。对比安培力的表达式，在去掉场源电流元的角标后，电流元的磁感应强度为：$d{\mathbf{B}} = k\frac{{Id{\mathbf{l}} \times {\mathbf{r}}}}{{{r^2}}}\\$

你发现没有，毕奥与萨伐尔找出的电流元对磁极的作用力表达式与上面的结果一模一样。

这是必然的嘛，因为按照场的观点，他俩找到的本就是电流元的磁感应强度的规律，只是他们以为这是力的表达式而已！所以在前面的表达式里就用了力的字母符号。

现在可以正式声明了：电流元的磁感应强度的结论被称为毕奥-萨伐尔定律！在国际单位制里，比例系数

$k = \frac{{{\mu _0}}}{{4\pi }}\\$

即有

$d{\mathbf{B}} = \frac{{{\mu _0}}}{{4\pi }}\frac{{Id{\mathbf{l}} \times {\mathbf{r}}}}{{{r^2}}}\\$

这里的常数${\mu _0} \approx 1.256 \times {10^{ - 6}}H/m$称为 真空磁导率 。

在 上篇文章 里已经说过矢量叉乘的方向特点，所以电流元的磁场在空间某处的磁感应强度方向与该电流元的方向垂直、同时还与电流元指向该处的连线垂直。高中生必备的右手螺旋定则通俗易懂地解决了这个问题。

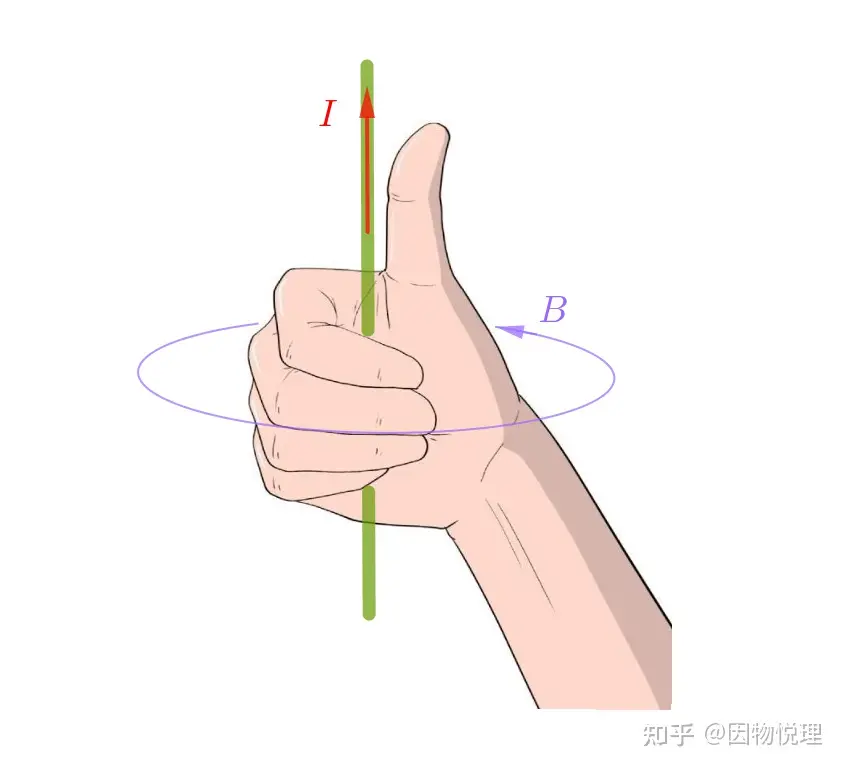
通电直导线的磁场方向与电流方向满足右手螺旋定则

至于放入该磁场中的检验电流元所受的安培力，则由高中生必备+1的左手定则给拿捏了。所以，跟着我左手右手一起用起来，安培力的表达式里面那两个吓死人的叉乘就变成了纸老虎。

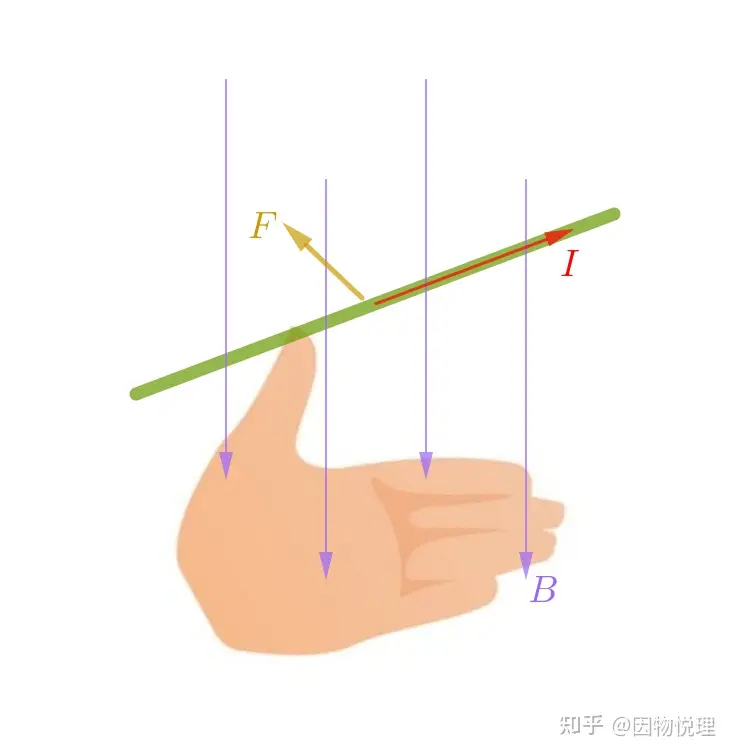
左手定则

毕奥-萨伐尔定律可以看成是静磁学里的火种。因为磁因电而生，如今得到了电流元所激发磁场的磁感应强度，而一般电流可以看成是大量电流元的集合，所以一般电流所激发的磁场就是所有电流元单独激发的磁场的矢量和。

如此说来，要得到一般电流所激发磁场的磁感应强度岂在话下？呃，理想和现实还是有差距的，微积分表示我才不背这个锅！

所以，咱们依然希望找到一些好用的定理去解决实际问题。

磁场的高斯定理和环路定理

和电场线的作用类似，磁感线是用来形象描述磁场的工具。通电直导线是最简单的场源电流，根据右手螺旋定则可以很清楚地看到它的磁感线是封闭曲线。这意味着对于任意的闭合曲面来说，当有多少条磁感线穿入这个闭合曲面，就有多少条磁感线穿出这个闭合曲面。

想到了啥？说明通电直导线所激发的磁场对于任意闭合曲面来说，磁通量均为零！

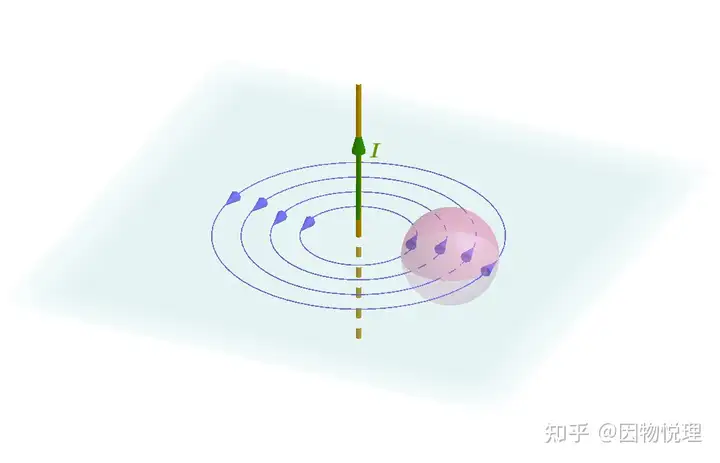
磁感线通过闭合曲面的示意图

严格的数学证明会确保从特殊到一般的正确性：磁场对于任意的闭合曲面的磁通量都为零。即有：

$\mathop{{ \oiint}}\limits_S {{\mathbf{B}} \cdot d{\mathbf{S}} = 0} \\$

哟，这不是矢量场的通量特点嘛？于是磁场的高斯定理申请加入麦氏集团。

再来瞅瞅磁场的环量特征。和静电场类似，磁场也有环路定理，不过与静电场的特点不同，磁场沿着某条闭合回路的积分结果并不为零。

咱们还是先看无限长通电直导线这个特殊例子。根据右手螺旋定则可知，无限长通电直导线激发的磁场，其磁感线是一系列以直导线为轴的同心圆。选择其中一条距轴半径为rrr的圆环路径，根据毕奥-萨伐尔定律使用积分运算就能得到此路径上各处的磁感应强度大小均为：

$B = \frac{{{\mu _0}I}}{{2\pi r}}\\$

而根据右手螺旋定则，半径为$r$的圆环路径上任意位置处的磁感应强度方向都与该处的线元$d{\mathbf{l}}$方向一致，所以无限长通电直导线的磁场在这条闭合圆轨迹上的环量为：

$\oint\limits_L {{\mathbf{B}} \cdot d{\mathbf{l}} = B \cdot 2\pi r = {\mu _0}I} \\$

数学再次给一般情形兜底，磁场的环路定理即为：恒定磁场沿任意闭合轨迹的环量均为

$\oint\limits_L {{\mathbf{B}} \cdot d{\mathbf{l}} = {\mu _0}I} \\$

式子里的III是此条闭合轨迹所围绕的电流。

这里强调恒定磁场是想强调激发磁场的电流是恒定的，因为变化的电流会激发变化的磁场，环路定理会变得不一样。不信你仔细瞅瞅，此处的环路定理和麦克斯韦方程组里的方程略有差异。不急，暂时搁置争议。

电荷守恒定律

电荷守恒定律的发现可有些年头了，18世纪40年代就被富兰克林提出来，就是那个雷雨天放风筝做实验的大佬。后续经过大量实验证明，一个与外界没有电荷交换的系统，正负电荷的代数和在任何物理过程中始终保持不变。

换句话说，即便这个系统与外界有电荷交换，一方得到多少电荷，则另一方就会失去多少电荷。

这就好比你的私有金库，你既不往里存钱也不用钱，金库里的钱就不变；要是上交给你的对象，不好意思啦，你的对象得到多少钱，你的私有金库就得流出多少钱！

电荷的定向移动形成电流

电荷在不同物体之间发生交换时就会发生定向移动，由此就会产生电流。虽然上图情形的电流只会存在短暂的时间，不过初中生都知道，只要能维持两个导体间的电压，那么图中导线里的电流就能持续存在，于是这就形成了一个含有电源的闭合电路。

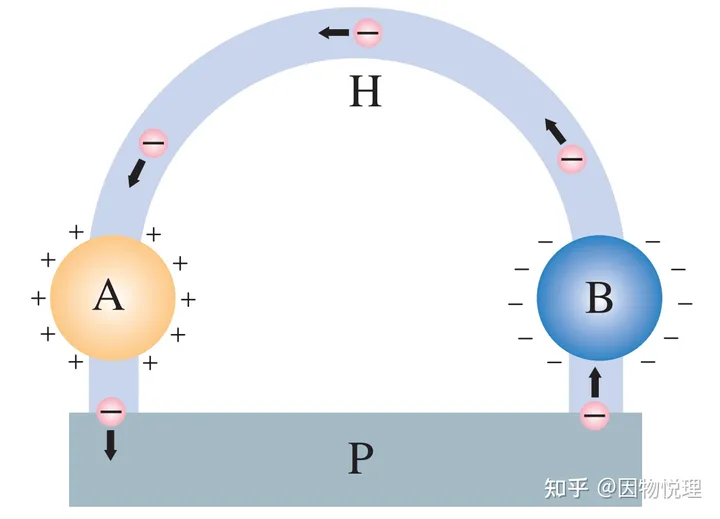
图中的P即为电源，它能使得闭合回路里形成持续的电流

对于电路里的电流来说，其强弱如何是咱们很关心的特点，所以得定义一个物理量去衡量，这就是电流强度I，简称电流。

电流的定义方式和速度的定义非常类似，看的是单位时间里定向移动穿过导体某一横截面的电荷量，即$I = \frac{q}{t}\\$不知各位在高中学到这个定义的时候，有没有觉得意犹未尽：既然提到了导体的某一横截面，为啥在电流的定义式里却没有体现出来？

虽然电流的微观表达式里会出现横截面的面积大小，但我想表达的是：导体截面要是比较大的话，此截面上不同部位的电流会不会有所差别呢？

这好比高速路口的收费站，现在大部分通道都是ETC通道，但是也保留了个别的人工通道。如果咱们观察车辆的通行情况，ETC通道肯定要比人工通道流畅！

其次，虽然我们口口声声说电流的流向如何，但却说它是个标量，这很令高中生头晕。毕竟从电流的定义可以发现，电量和时间都是标量，你没法让它俩定义出来的电流是矢量呀！但是电流确实沿着导线有方向的流动着，所以咱们需要一个矢量来描述方向性。

为了解决上述这些问题，还有一个物理量得定义出来，称为电流密度${\mathbf{j}}$。

顾名思义，电流密度是单位横截面上通过的电流大小，但是这个单位横截面有要求——必须是垂直于电流方向的单位横截面。另外，作为矢量的电流密度，其方向定为与导体中各点处的电流方向相同。

所以电流密度${\mathbf{j}}$满足

$dI = {\mathbf{j}} \cdot d{\mathbf{S}}$

式子里的$d{\mathbf{S}}$是垂直于电流方向的面积元。

那么通过导体中任意截面S的电流I与电流密度的关系则为

$I = \iint\limits_S {{\mathbf{j}} \cdot d{\mathbf{S}}}\\$

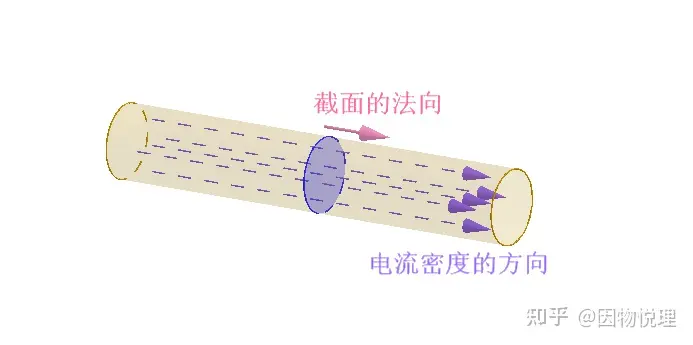
电流密度的示意图

你看上图熟悉不？这一茬茬有向箭头是不是和电场线很像？好吧，起名为电流线喽。与电场线表示电场强度方向一样，电流线上每点的切线方向都和该点的电流密度方向一致。

有了电流密度与电流的关系，电荷守恒定律在电流中的体现就能写出来啦。你在导体内任取一个闭合曲面S，由电荷守恒定律就很容易知道：在某段时间里由此面流出的电量等于这段时间里S面内所包含的电量的减少量。

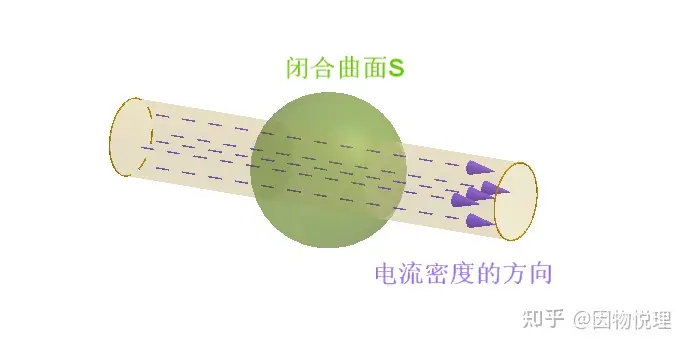
电流连续性的示意图

老规矩，取S面上各处的法线正方向朝外侧，则单位时间里由S面流出的电量等于

$\mathop{{ \oiint}}\limits_S {{\mathbf{j}} \cdot d{\mathbf{S}}} \\$

若S面内$dt$时间里的电量增量为$dq$的话，那么单位时间里S面内的电量减少为$- \frac{{dq}}{{dt}}\\$

所以就有等式

$\mathop{{ \oiint}}\limits_S {{\mathbf{j}} \cdot d{\mathbf{S}}} = - \frac{{dq}}{{dt}}\\$

这便是电流 连续性方程 ，其本质就是电荷守恒定律的体现。

咋一看去，麦克斯韦方程组与电流连续性方程好像毫无关系，不过两者里面都出现了电流密度，或许它们之间还是有点瓜葛吧。不着急，先放一放。

法拉第电磁感应定律

至从奥斯特的实验揭示了电流的磁效应后，磁生电的愿望就一直萦绕在人们的心头。关于法拉第十年磨一剑去探寻磁生电的故事应该是众所周知的，在尝试了各种方案后，实验终于在1831年的时候出现了重大突破，梦寐以求的感应电流终于出现了！

领悟到产生感应电流的条件后，法拉第很快发现了产生感应电流的多种情形。如何把这些不同情形的共有特点给提炼出来，这就很考验一个人的洞察力了。

法拉第不负众望地完成了这个使命：他发现只要穿过闭合电路的磁通量发生了变化，闭合电路中就能产生感应电流。而感应电流的大小并不取决于穿过闭合电路的磁通量大小，而是取决于磁通量的变化快慢！

不仅如此，他还在实验中发现，磁通量变化相同的条件下，不同金属导体中的感应电流大小与金属导体的电阻成反比。

在此之前， 欧姆定律 ，而感应电动势才是各种情形里产生感应电流的背后推手！

更厉害的是，他已经确信即使电路没有闭合、甚至没有电路的存在，电磁感应现象依然会产生感应电动势！闭合电路只是把感应电动势以感应电流的形式给体现出来了而已！天呐，法拉第此时已经触摸到了电磁学的精髓，只待后来者给出精确地数学描述。

有了法拉第的正确思想做指导，电磁感应定律的数学表达式最终被确定下来——感应电动势的大小正比于穿过闭合电路的磁通量的变化率！即有

$E = - k\frac{{d\Phi }}{{dt}}\\$

比例系数$k$的值由所选择的单位制决定，在国际单位制里有$k = 1$。

再把磁通量的计算式带入进去，则感应电动势可以写成

$E = - \frac{d}{{dt}}\iint\limits_S {{\mathbf{B}} \cdot d{\mathbf{S}}}\\$

给你抛出一个问题：你觉得感应电动势是矢量还是标量？你看上面的式子，磁通量和时间都是标量，由它两算出的变化率也是标量，所以感应电动势是标量！但是在一般场合里却会说这个负号表示感应电动势的方向！有点离谱了不是？

此处需要稍微啰嗦一下。电源的作用是维持电路里的电压，其本质上是一个能量转化装置——把其他形式的能量转化为电能。为了体现这种能量转化的本领才引入了电动势的概念：在电源内部把单位正电荷从负极移到正极时，非静电力所做的功。

想必高中生都很清楚它的定义式为

$E = \frac{W}{q}\\$

这里的$W$是电源内部的非静电力做的功。电源的类型不同，非静电力的机制也不一样，马上你就会明白。

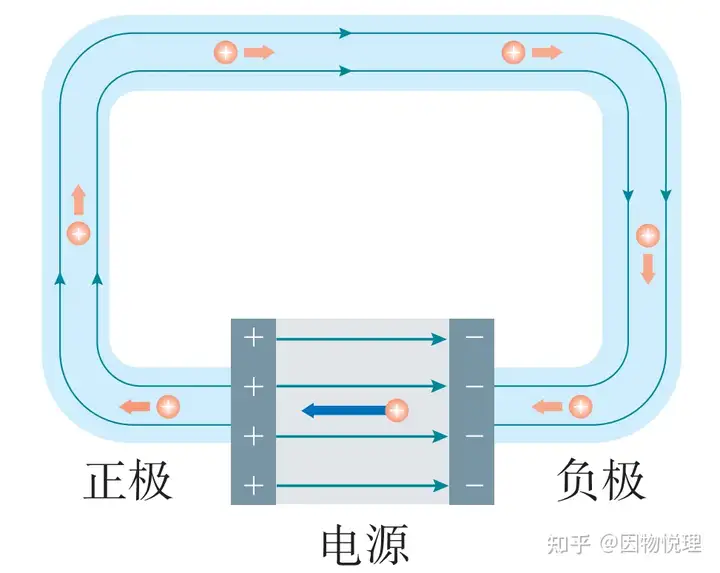
电源内部的非静电力及其作用

根据电动势的定义，电源内部的非静电力方向必然是负极指向正极的，所以非静电力存在方向这一说。

话说到了这个份上，你应该明白电磁感应定律的表达式里，负号其实反映的是非静电力的方向！它的方向直接决定了闭合回路中的感应电流的方向！

至于感应电流的方向如何判断，精辟至极的 楞次定律]给你送上——闭合回路里感应电流的方向，总是使得它激发的磁场来阻碍引起感应电流的磁通量的变化！“来拒去留，增反减同”的八字口诀应该深深留在了高中生的脑海里吧？

正是因为电磁感应现象的出现会阻碍原磁通量的变化，那么原磁通量要继续变化就需要外界提供能量；也只有原磁通量继续变化，电磁感应现象才会持续存在。很显然，这个负号把能量守恒的特点体现得淋漓尽致。

说完公式里的负号问题，接下来就该说点大事情了！从法拉第的实验来看，能产生电磁感应现象的情形可以分为两大类：第一类是在恒定磁场中运动的导体内所产生的感应电动势；另一类是导体不动，因磁场的变化而产生的感应电动势。

第一类情形的感应电动势之所以存在，本质上是因为导体内的自由电荷在随导体棒运动时受到了磁场施加的[洛伦兹力]，它充当着非静电力的角色。而第二类情形里，自由电荷所受的非静电力就大有来头了。

现在咱们必须给麦神正名——他可不是[拿来主义]！虽然他的方程组里有两个都是高斯定理的结论，这是基于麦克斯韦发现了通量能描述矢量场的特征，他才从众多的公式中选择了两个高斯定理的结论。

所以呀，不是谁都能够做到透过现象看到本质，咱们可不能事后诸葛去评论当初的事态发展，况且接下来就到了麦神真正施展才华的时刻。

涡旋电场与[位移电流]

对于第二类情形里的非静电力，麦克斯韦敏锐地意识到这是变化磁场本身所引起的——无论导体是否存在，变化的磁场会在其周围激发一种电场！当有闭合导体存在时，这种电场作用于其内部的自由电荷并使之产生定向运动，从而在闭合电路中产生感应电流。

这种由变化磁场所激发出来的电场与静电场不同，一是因为它不是由电荷激发的；二是因为它的电场线必然是闭合的！不然的话，受它作用的自由电荷怎能在闭合导体内持续定向移动呢？

于是这种电场被称为感应电场或者是涡旋电场。涡旋电场作用于自由电荷的力不是静电力，那自然就得归入到非静电力的阵营啦。

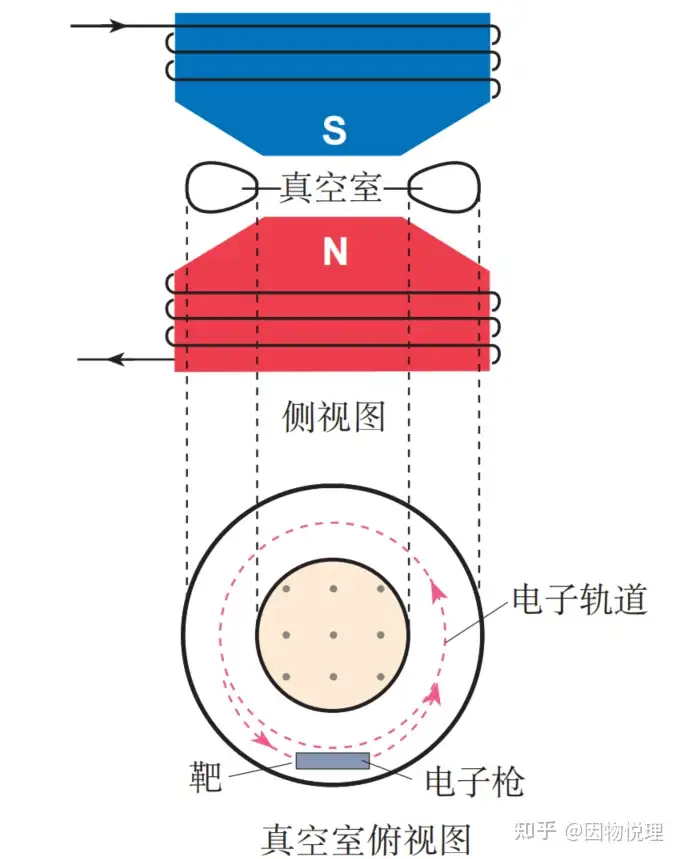
电子感应加速器的示意图，该装置利用涡旋电场加速电子

相比法拉第对感应电动势的认识，麦神直接上升到涡旋电场的高度，你现在有对麦神的洞察力刮目相看了吗？请先收好你的膝盖，后面会让你膜拜得更久。咱们先看看涡旋电场满足什么规律吧。

既然涡旋电场作用于自由电荷的力为非静电力，则对于闭合回路而言，非静电力做功的结果等于
$W = \oint\limits_L {q{\mathbf{E}} \cdot d{\mathbf{l}}} \\$

而根据电动势的定义，非静电力做功为
$W = qE$

再联合法拉第电磁感应定律可知

$\oint\limits_L {{\mathbf{E}} \cdot d{\mathbf{l}}} = - \frac{d}{{dt}}\iint\limits_S {{\mathbf{B}} \cdot d{\mathbf{S}}}\\$

由于这种情形里只有磁场在变化，所以此式的右边可以改写成

$\oint\limits_L {{\mathbf{E}} \cdot d{\mathbf{l}}} = - \iint\limits_S {\frac{{\partial {\mathbf{B}}}}{{\partial t}} \cdot d{\mathbf{S}}}\\$

之所以写成$\frac{{\partial {\mathbf{B}}}}{{\partial t}}$而不是$\frac{{d{\mathbf{B}}}}{{dt}}$，是因为磁场${\mathbf{B}}$不仅随时间变化，它还受到位置的影响（难道不同位置的磁感应强度必须一样吗？），$\frac{{\partial {\mathbf{B}}}}{{\partial t}}$表示的是同一位置的${\mathbf{B}}$随时间$t$的变化率。

对了，你还记得静电场的环路定理吗？静电场沿某一闭合路径积分的结果为零。对于刚刚得到的上式，如果磁场不随时间变化，那么上式右侧的结果即为零。

所以上式可以把静电场的环路定理给统一起来，形成描述电场环量特点的通项式，因此被荣幸纳入麦氏方程组的是它而不是静电场的环路定理！

最后再来说说麦氏封神的观点。前面提到磁场的环路定理是针对恒定电流的磁场而言，即恒定电流激发的磁场满足

$\oint\limits_L {{\mathbf{B}} \cdot d{\mathbf{l}}} = {\mu _0}I\\$这里的III是穿过以闭合曲线LLL为边界的电流。

然而 上篇文章 里就说过，以闭合曲线LLL为边界的曲面SSS可以有任意多个！而对于其中任意一个曲面$S$来说，都有

$I = \iint\limits_S {{\mathbf{j}} \cdot d{\mathbf{S}}}\\$

既然如此，咱们完全可以像下图这样以LLL为边界左右分别取两个不同的曲面${S_1}$和${S_2}$，则肯定有

$\iint\limits_{{S_1}} {{\mathbf{j}} \cdot d{\mathbf{S}}} = \iint\limits_{{S_2}} {{\mathbf{j}} \cdot d{\mathbf{S}}}\\$

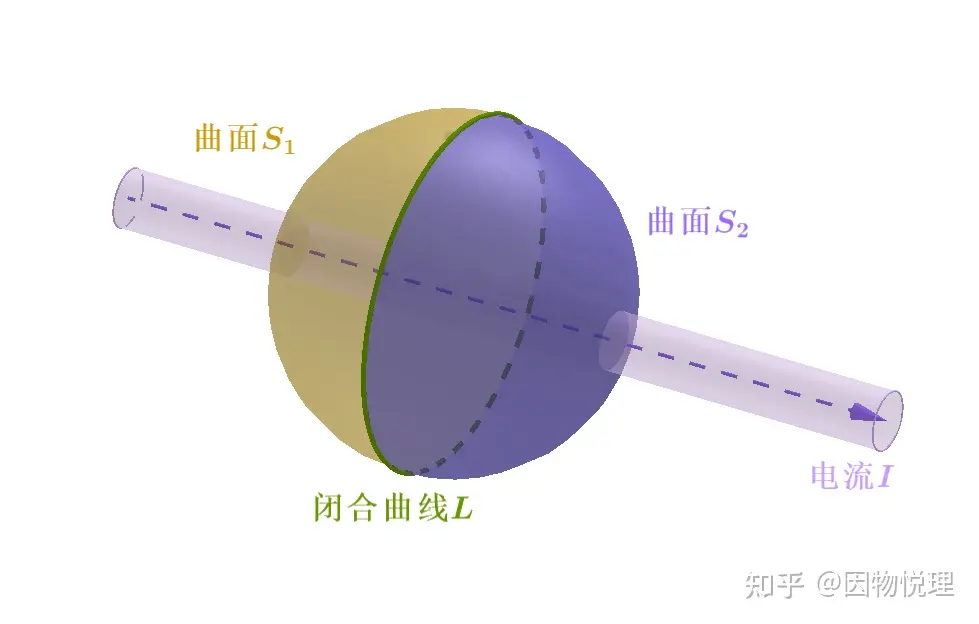
同一条闭合曲线可以对应无数个以它为边界的曲面

由于咱们颇有心机地选择，使得两个曲面S1{S_1}{S_1}和S2{S_2}{S_2}正好形成一个封闭曲面，这一进一出的电流密度通量相等，不就有

$\mathop{{ \oiint}}\limits_S {{\mathbf{j}} \cdot d{\mathbf{S}}} = 0\\$

么？

显然这是电流连续性特征

$\mathop{{ \oiint}}\limits_S {{\mathbf{j}} \cdot d{\mathbf{S}}} = - \frac{{dq}}{{dt}}\\$
在恒定电流情形下的必然结果。

因为电路中通有恒定电流时，电路中任何地方的电荷都是处于“收支平衡”的恒定状态，所以$\frac{{dq}}{{dt}}{\text{ = }}0\\$

也就是说对于恒定电流来说，磁场的环路定理和电荷守恒定律是和平共处的。不过这个和谐美好的局面在含容电路面前破防了。

电路中含有电容器时，电容器会存在充电与放电过程，此过程中的电流是变化的。由于电容器两极板之间是彼此绝缘的，所以板间区域没有电流。

如果咱们像图中这样针对同一条闭合曲线LLL选取两个不同的闭合曲面，则在计算磁场的环量$\oint\limits_L {{\mathbf{B}} \cdot d{\mathbf{l}}} \\$时必然会出现不同的结果！

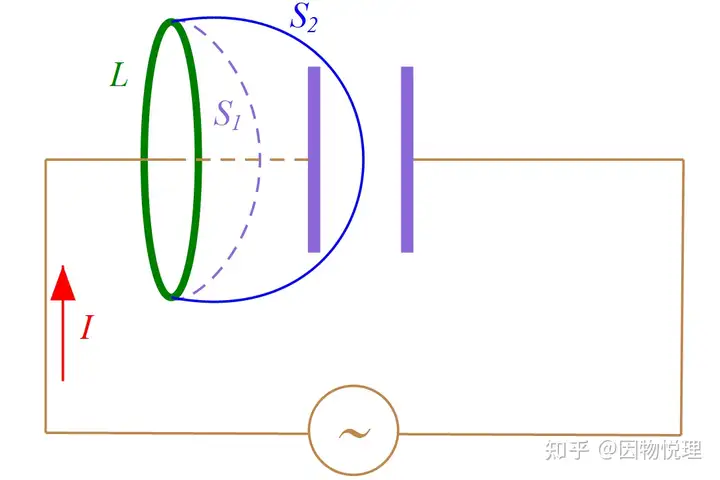
含容电路暴露出磁场的环路定理的内部矛盾

因为对于曲面${S_1}$来说有
$\iint\limits_{{S_1}} {{\mathbf{j}} \cdot d{\mathbf{S}}} \ne 0\\$
而对曲面${S_2}$来说则有
$\iint\limits_{{S_2}} {{\mathbf{j}} \cdot d{\mathbf{S}}} = 0\\$

这意味着选择曲面${S_1}$时算得
$\oint\limits_L {{\mathbf{B}} \cdot d{\mathbf{l}}} \\$
的结果不为零，但是选择曲面${S_2}$时算得
$\oint\limits_L {{\mathbf{B}} \cdot d{\mathbf{l}}} \\$
的结果却为零！这与磁场的环路定理相矛盾！

电容器的出现制造了磁场的环路定理的内部矛盾，怎样消除这个矛盾便是当务之急。守恒现象被认为是普遍的规律，既然您包罗万象，那就大人有大量，去哄哄人家那个磁场的环路定理呗。

所以咱们依然认定电流的连续性方程

$\mathop{{ \oiint}}\limits_S {{\mathbf{j}} \cdot d{\mathbf{S}}} = - \frac{{dq}}{{dt}}\\$

成立，只是在上图的闭合曲面里，电容器极板上的电量会随着充、放电过程的进行而时刻发生改变，所以电荷的变化率不为零。

至于极板上的电量有多少，这不有电场的高斯定理

$\mathop{{ \oiint}}\limits_S {{\mathbf{E}} \cdot d{\mathbf{S}} = \frac{q}{{{\varepsilon _0}}}} \\$

么？等式里的${\mathbf{E}}$就是电容器极板间的电场强度。

联合电流的连续性方程就有

$\mathop{{ \oiint}}\limits_S {{\mathbf{j}} \cdot d{\mathbf{S}}} = - {\varepsilon _0}\frac{d}{{dt}}\mathop{{ \oiint}}\limits_S {{\mathbf{E}} \cdot d{\mathbf{S}}} \\$
在电容器充、放电的过程里，板间的场强会随时间变化，所以上式右侧的求导结果可以写成

$\frac{d}{{dt}}\mathop{{ \oiint}}\limits_S {{\mathbf{E}} \cdot d{\mathbf{S}}} = \mathop{{ \oiint}}\limits_S {\frac{{\partial {\mathbf{E}}}}{{\partial t}}} \cdot d{\mathbf{S}}\\$

写成$\frac{{\partial {\mathbf{E}}}}{{\partial t}}$的原因是闭合曲面虽然可以任意选取，但是咱们一旦选好了，它就不随时间变化；而场强${\mathbf{E}}$显然是位置与时间的函数，我们现在关心的是某一点的场强随时间变化的情况！这与法拉第电磁感应定律里出现$\frac{{\partial {\mathbf{B}}}}{{\partial t}}$的原因一样。

可以来瞅瞅结果了。把求导后的结果带入原式，移项就有

$\mathop{{ \oiint}}\limits_S {({\mathbf{j}} + {\varepsilon _0}\frac{{\partial {\mathbf{E}}}}{{\partial t}}) \cdot d{\mathbf{S}}} = 0\\$

有点眼熟吧？没错，像极了之前的结论

$\mathop{{ \oiint}}\limits_S {{\mathbf{j}} \cdot d{\mathbf{S}}} = 0\\$

不过此处的式子才是完全体！名曰全电流在任何情形下都是连续的。等等，什么是全电流？

在电路里，**由电荷定向移动形成的电流是正儿八经的电流，也称为 传导电流 **。鉴于上面这个等式，麦克斯韦认为

${\varepsilon _0}\frac{{\partial {\mathbf{E}}}}{{\partial t}}\\$应该是某种电流密度，冠名之** 位移电流密度 **。

自然的，式子

$\iint\limits_S {{\varepsilon _0}\frac{{\partial {\mathbf{E}}}}{{\partial t}} \cdot d{\mathbf{S}}}\\$

就是位移电流喽。这是麦克斯韦具有独立知识产权的重要假设！

于是传导电流与位移电流之和就是全电流！虽然位移电流密度有“电流”之名，但却与电荷毫无关系，因为它是电场随时间的变化率。不过这个名字既然被麦神用了，那就延续下去吧。

在有了全电流连续性的假设后，随之而来就得把磁场的环路定理改成：

$\oint\limits_L {{\mathbf{B}} \cdot d{\mathbf{l}}} = \iint\limits_S {{\mu _0}({\mathbf{j}} + {\varepsilon _0}\frac{{\partial {\mathbf{E}}}}{{\partial t}}) \cdot d{\mathbf{S}}} \\$

显然，当电场随时间的变化率为零时，这个方程就能退化成静磁场的环路定理。于是，通吃磁场环量特点的结论诞生了，麦神请收货。

这个等式不仅仅只是消除了磁场环路定理的内部矛盾，它更是坐实了电场与磁场间如胶似漆的关系！

你看嘛，**这个等式表明位移电流和传导电流一样也能激发磁场，本质上说明了变化的电场会激发磁场。而法拉第电磁感应定律表明，变化的磁场会激发电场。 完美的对称 **！

如果两者就这么互相地激发，一个新的事物——电磁波就诞生了！这正是麦神留给世界的一个预言。

遗憾的是，英年早逝的麦神没能亲眼见证到电磁波被赫兹的实验给证实。位移电流的假设随着电磁波的发现而被正名，你还敢说麦克斯韦是拿来主义吗？

麦神的成果完美体现了物理学的发展逻辑——从实验上升到理论，由理论去预言（指导）实践。这是多么漂亮的左右互搏、共同进步啊！

麦克斯韦方程组

行文至此，咱们已经对两个环路定理进行了推广，但是对两个高斯定理没动手脚。这是因为两个高斯定理虽然是针对静场总结的规律，但是它俩与整个理论不存在不自洽，也不与实验冲突，所以麦克斯韦默认它俩对 时变电磁场 也是成立的。

至于假定是否正确，可以由方程组推出的结论的正确性去保证。这个后面再说。咳咳，障碍全部扫清，是时候亮出麦克斯韦方程组（积分形式）啦！

电场的高斯定理：

$\mathop{{ \oiint}}\limits_S {{\mathbf{E}} \cdot d{\mathbf{S}}} = \frac{Q}{{{\varepsilon _0}}}\\$

电场的环路定理：

$\oint\limits_L {{\mathbf{E}} \cdot d{\mathbf{l}}} = - \iint\limits_S {\frac{{\partial {\mathbf{B}}}}{{\partial t}} \cdot d{\mathbf{S}}} \\$

磁场的高斯定理：

$\mathop{{ \oiint}}\limits_S {{\mathbf{B}} \cdot d{\mathbf{S}} = 0} \\$

磁场的环路定理：

$\oint\limits_L {{\mathbf{B}} \cdot d{\mathbf{l}}} = \iint\limits_S {{\mu _0}({\mathbf{j}} + {\varepsilon _0}\frac{{\partial {\mathbf{E}}}}{{\partial t}}) \cdot d{\mathbf{S}}} \\$

发现没，这四个方程的核心就是围绕着矢量的通量与环量展开：两个高斯定理就是揭示通量特点的定理；而两个环路定理就是揭示环量特点的定理。咋样，麦神的方程组（积分形式）理解起来是不是也很容易呢？

结合我写的《 什么是向量 很容易转换成微分方程。毕竟微分方程用起来更方便一些。

积分形式的方程是从宏观层面来描述电磁场的特点，落脚点是矢量的通量与环量；而 微分形式 的方程则是把注意力集中于电磁场中的某个点，你大概应该猜到了落脚点是矢量的散度与旋度吧？

既然要研究某点处的电磁场规律，对于积分形式的方程来说，咱们就得把闭合曲面或者闭合曲线所包围的区域不断缩小，直到为一个点。考虑到你们可能懒得去翻看我的 上篇文章 ，这里就直接把即将要用到的结论再贴一遍吧。

某个矢量${\mathbf{v}}$的通量与它的散度存在关系

$\iiint\limits_V {(\nabla \cdot {\mathbf{v}})dV} = \mathop{{ \oiint}}\limits_S {{\mathbf{v}} \cdot d{\mathbf{S}}} \\$

大名鼎鼎的高斯定理在此。虽然名称与场的高斯定理高度雷同，但是等式内容不一样哟。

某个矢量${\mathbf{v}}$的环量与它的旋度存在关系

$\iint\limits_S {(\nabla \times {\mathbf{v}}) \cdot d{\mathbf{S}}} = \oint\limits_L {{\mathbf{v}} \cdot d{\mathbf{L}}} \\$

如雷贯耳的 斯托克斯公式 前来报到。

别担心，接下来的数学推演很简单，来都来了，别跑哈。由高斯定理，电场强度对于某个闭合曲面的通量可以写成

$\mathop{{ \oiint}}\limits_S {{\mathbf{E}} \cdot d{\mathbf{S}}} = \iiint\limits_V {\left( {\nabla \cdot {\mathbf{E}}} \right)dV}\\$

右边式子里的VVV就是该闭合曲面所包围的体积。

至于该闭合曲面里的电荷量可以写成
$Q = \iiint\limits_V {\rho dV}\\$这里的$\rho$ 被称为电荷的体密度。

于是电场的高斯定理就变成了$\iiint\limits_V {\left( {\nabla \cdot {\mathbf{E}}} \right)dV} = \frac{1}{{{\varepsilon _0}}}$

好好的电场的高斯定理被改写成这样，咋越看越复杂了？别急，由于改写之前的等式针对任意闭合曲面都成立，所以咱们可以把这个闭合曲面取得任意小，直到它趋于一个点！于是就有
$\nabla \cdot {\mathbf{E}} = \frac{\rho }{{{\varepsilon _0}}}\$
电场的高斯定理的微分形式就这么轻松搞定啦。

同样的办法，不难得到磁场的高斯定理的微分形式为$\nabla \cdot {\mathbf{B}} = 0\\$

顺便沾个光，电流连续性方程

$\mathop{{ \oiint}}\limits_S {{\mathbf{j}} \cdot d{\mathbf{S}}} = - \frac{{dq}}{{dt}}\\$

虽然不在麦氏家族群里，但同样的办法改造一下这个方程，也能得到其微分形式：
$\nabla \cdot {\mathbf{j}} = - \frac{{\partial \rho }}{{\partial t}}\\$

电荷量对时间的微商之所以变成了电荷体密度对时间的偏导，是因为电荷体密度不仅与时间有关，还与位置有关。微分形式的方程着眼于一个点，所以位置是确定的，这才把对时间的微商改写成对时间的偏导。

再来说两个环路定理。由斯托克斯公式，电场强度对于某条闭合曲线的环量可以写成

$\oint\limits_L {{\mathbf{E}} \cdot d{\mathbf{L}}} = \iint\limits_S {\left( {\nabla \times {\mathbf{E}}} \right)} \cdot d{\mathbf{S}} \\$

所以电场的环路定理就变成了

$\iint\limits_S {\left( {\nabla \times {\mathbf{E}}} \right)} \cdot d{\mathbf{S}} = - \iint\limits_S {\frac{{\partial {\mathbf{B}}}}{{\partial t}} \cdot d{\mathbf{S}}} \\$

同样是因为改写之前的等式针对任意闭合曲线都成立，所以咱们可以把这条闭合曲线取得任意小，直到它趋于一个点！于是电场的环路定理的微分形式就变成了
$\nabla \times {\mathbf{E}} = - \frac{{\partial {\mathbf{B}}}}{{\partial t}}\\$

同样的办法，磁场的环路定理的微分形式就是
$\nabla \times {\mathbf{B}} = {\mu _0}({\mathbf{j}} + {\varepsilon _0}\frac{{\partial {\mathbf{E}}}}{{\partial t}})\\$

到此，更常用的麦克斯韦方程组的微分形式就全部得到了：

$\nabla \cdot {\mathbf{E}} = \frac{\rho }{{{\varepsilon _0}}} \\\nabla \times {\mathbf{E}} = - \frac{{\partial {\mathbf{B}}}}{{\partial t}} \\\nabla \cdot {\mathbf{B}} = 0 \\\nabla \times {\mathbf{B}} = {\mu _0}({\mathbf{j}} + {\varepsilon _0}\frac{{\partial {\mathbf{E}}}}{{\partial t}}) \\$

微分形式的方程看起来要比积分形式的方程简洁得多，而且从这组方程里可以得到一个及其重要的结论和预言：那就是电磁波的波速为$\frac{1}{{\sqrt {{\varepsilon _0}{\mu _0}} }}\\$这个结果在以后的文章里单独说明。

带入这两个常数进行计算就会发现，波速恰好等于光速$c$，即$c = \frac{1}{{\sqrt {{\varepsilon _0}{\mu _0}} }}\\$于是麦神大胆预言了光是电磁波！

结语

写到这，麦神的方程组该落下帷幕了。随着预言成真，方程组经受住了一波考验，但要想成为一个领域的统领还需面对更多的质疑，这不就有两个问题等着翻牌：

1、电磁波的波速虽然计算出来了，但是整个方程组里通篇不见参照物，那么这个波速是相对谁而言呢？毕竟咱们从初中开始接触物理的时候就知道，要描述运动必须选择参照物！

2、电磁感应现象里，动生电动势和 感生电动势 真的泾渭分明吗？