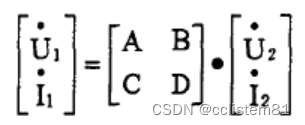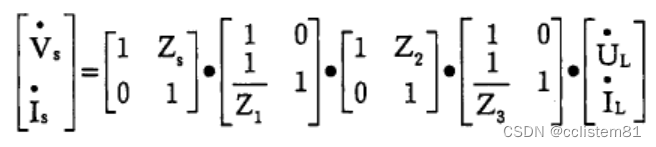一、二端口网络

对于EMI滤波器,使用二端口网络来进行数学描述
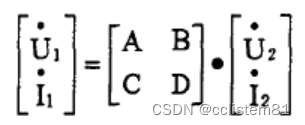
则滤波器中的任意一个电阻、电容、电感等元件都可以用一个二端口网络来描述,最后将各二端口网络串联起来,就能通过矩阵运算,得到整个滤波网络的二端口等效数学模型。
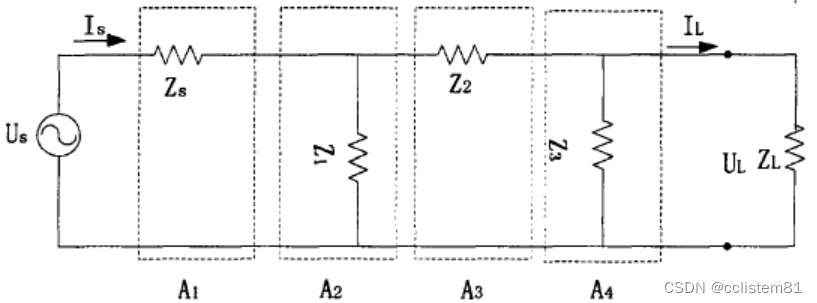
如下图所示,A1~A4为四个二端口网络,
其中,
A1=[10Zs1]
A2=[1Z1101]
A3=[10Z21]
A4=[1Z3101]
则整个二端口网络的数学表示
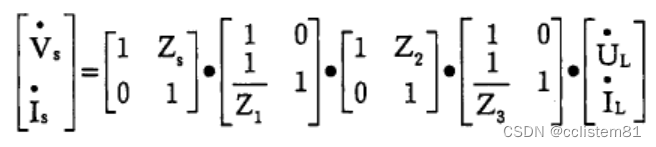
常用拓扑的二端口参数矩阵
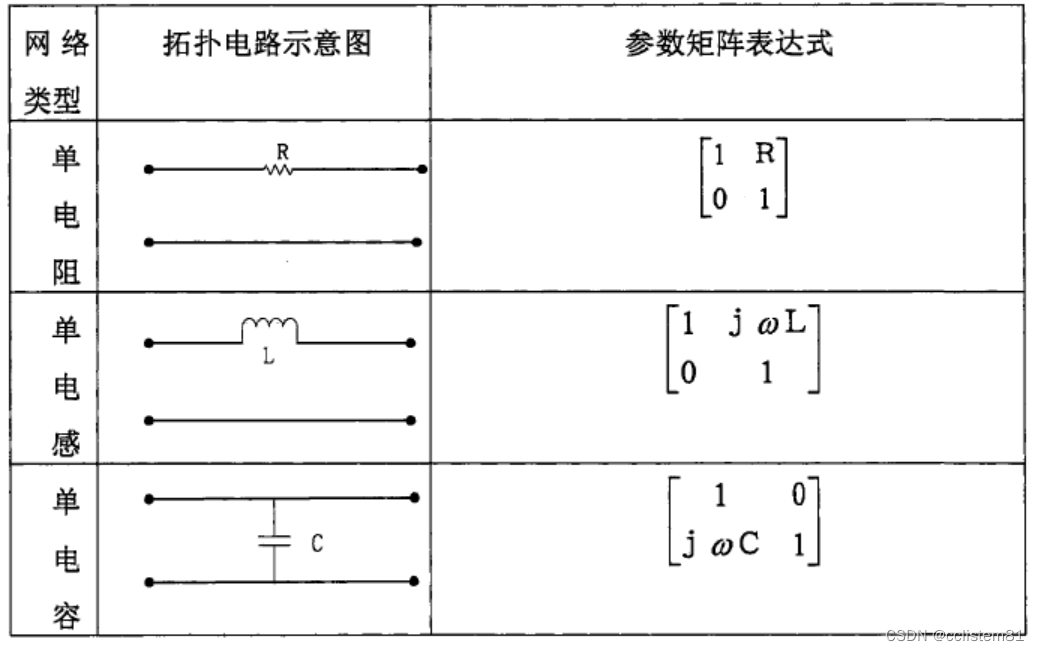
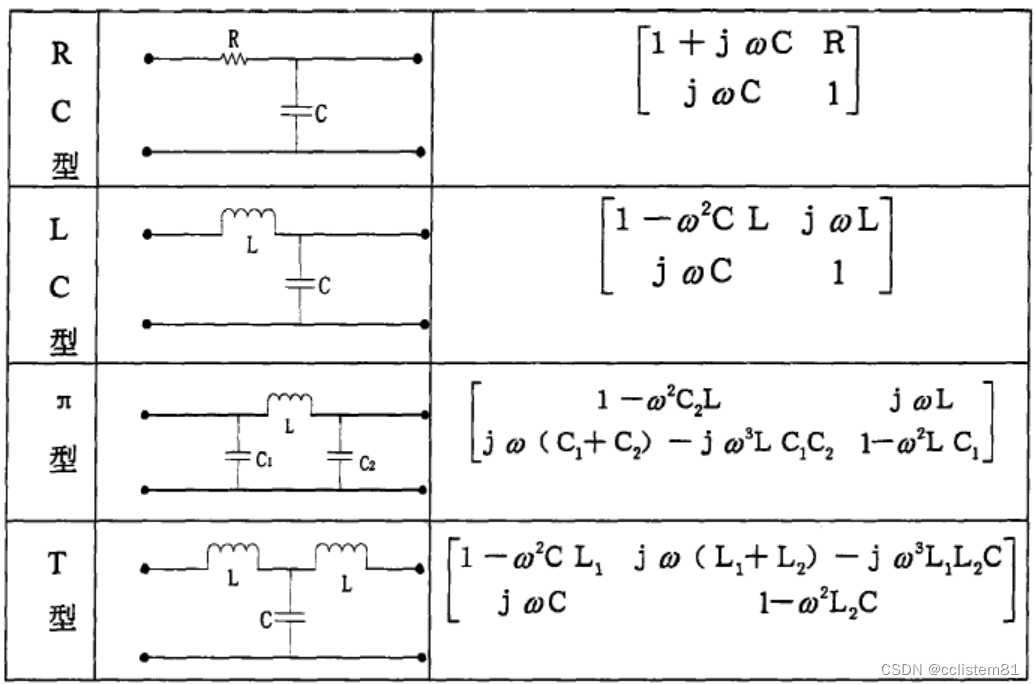
二、插入损耗
插入损耗=(未接EMI滤波器时电磁干扰源加到负载上的功率P1)/(接入EMI滤波器时电磁干扰源加到负载上的功率P2)
计算公式:
I⋅L=10lg(P2P1)
功率P1和P2的表达式为
P1=ZLV˙12
P2=ZLV˙22
其中V1为未加滤波器时,负载上的电压,V2为加滤波器之后,负载上的电压。
则插损表达式又可写为
I⋅L=10lg(V˙22V12˙)=20lg(V˙2V˙1)
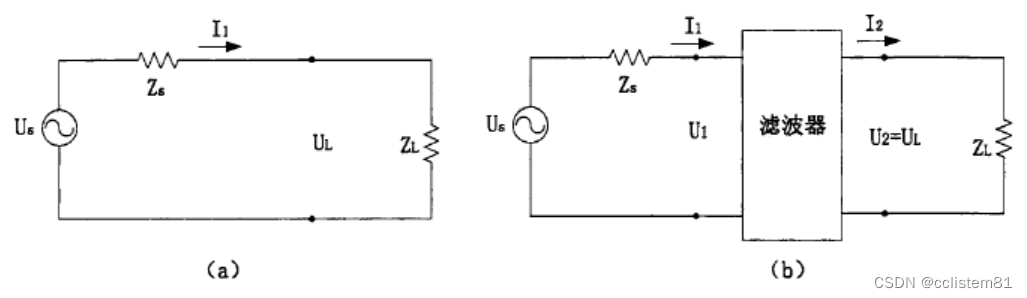
其中,由图a,
V˙1=Z˙s+Z˙LV˙2
对于图b,由上一节二端口网络原理
{U˙1=AV2˙+BI˙2I˙1=CV˙2+DI˙2
U˙1=U˙s−I˙1ZzV˙2=I˙2ZL
由上三式可推导出
V˙2=AZL+B+CZLZs+DZsU˙sZL
由V1和V2的表达式,可得插入损耗
I⋅L=20lg∣Zs+ZLAZL+B+CZLZs+DZs∣
其中的A,B,C,D就是上节二端口网络做的那个参数矩阵中的各个参数。
三、举例
1、LC滤波器
二端口网络数学表述

提取参数,列写插损表达式
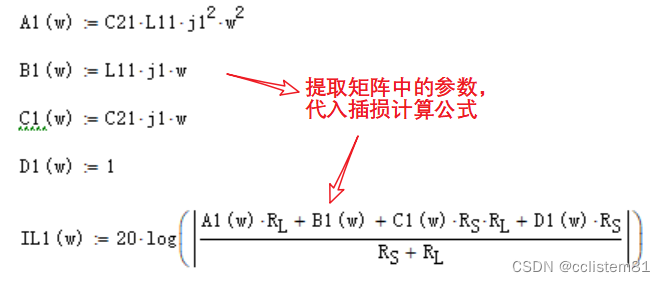
画图
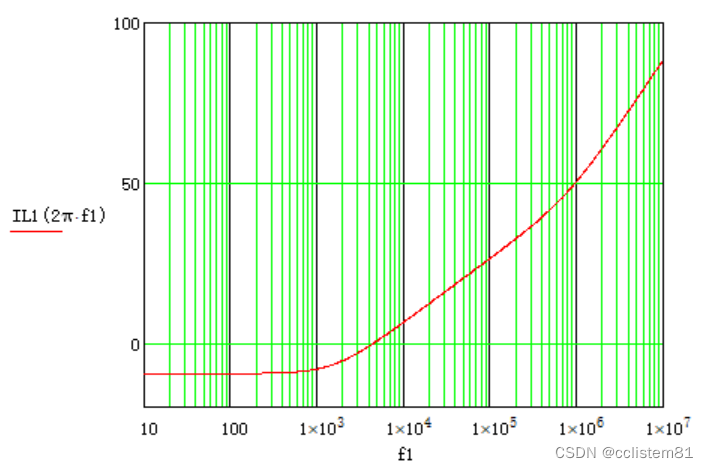
2、CLC滤波器
二端口表达

画图
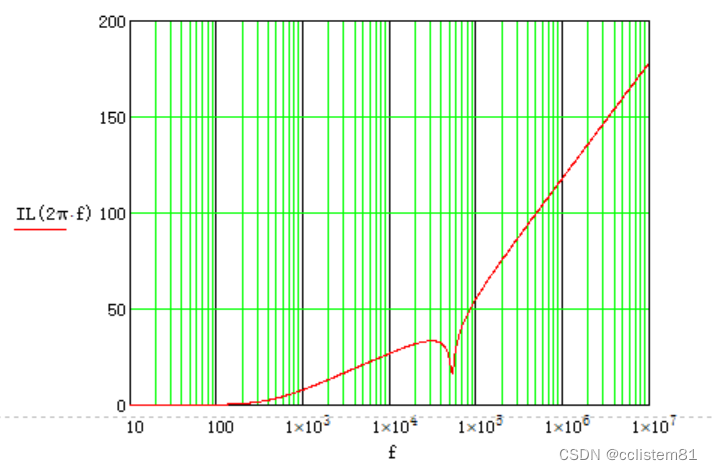
三、插损作用
根据目前变换器的传导超标程度,计算出所需的在某个频率点或频率段的所需最小差模插损和共模插损,然后进行滤波器阶数设计和参数设计,核算是否满足插损要求。