SEPIC(Single Ended Primary Inductor Converter)电路,是一种经典的DC-DC电源电路,从它的名字也能够看出,它的输入端串联了一个电感,因此能够减小输入电流纹波。说到输入串电感,不难想到Boost电路也具有这个特点,然而Boost只能实现升压,而SEPIC能够实现升降压。说到升降压,不难想到Buck-Boost电路,然而传统Buck-Boost的输出电压是反极性的,也就是输出负电压,这限制了Buck-Boost电路的应用范围,而SEPIC电路能够输出正极性电压。这些优点也使得SEPIC电路在当时取得了广泛的应用。
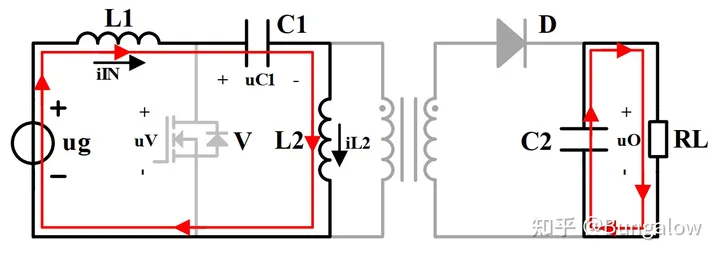
下图展示了带隔离变压器的SEPIC经典结构。
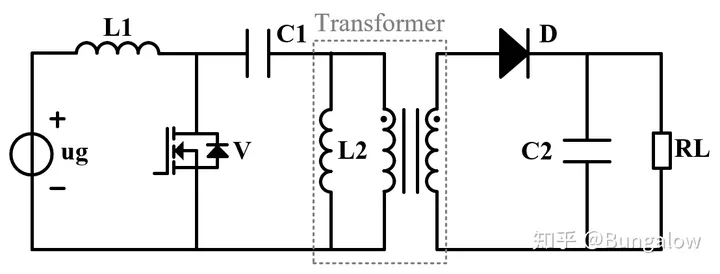
上图中, 𝑢𝑔 是输入电压, 𝑅𝐿 是负载电阻。注意,这里忽略了变压器原边和副边的电阻和漏自感以及励磁电阻(即忽略铁损),从而将仅剩的励磁电感 𝐿2 抽象出来。实际的励磁电感是一个随着磁芯饱和程度而变化的量,但这里暂且认为 𝐿2 为定值。 𝐿2 的后方是一个理想变压器,也可以认为就是一个用于电压折算的简单比例环节,电压增益为 𝑘 , 𝑘=𝑛2𝑛1 , 𝑛1 和 𝑛2 为变压器原边和副边线圈匝数。若不使用隔离变压器,而直接用电感取代,则认为 𝑘=1 。
一.电路工作状态分析
1.1 CCM(Continuous Current Mode)
由于电容两端电压不能突变且电容值较大,所以电容电压纹波一般较小,这里取每个电容在一个开关周期内的电压平均值代替其瞬时值,当电路稳定工作时,该平均值保持不变。
MOSFET开通时:
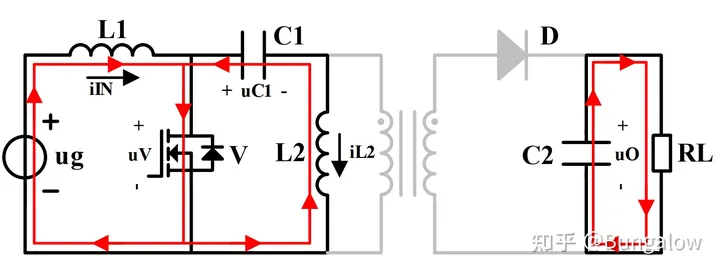
μL1(on)=μg (1-1)
uL2(on)=−uC1 (1-2)
iC1(on)=iL2 (1-3)
MOSFET截止时:
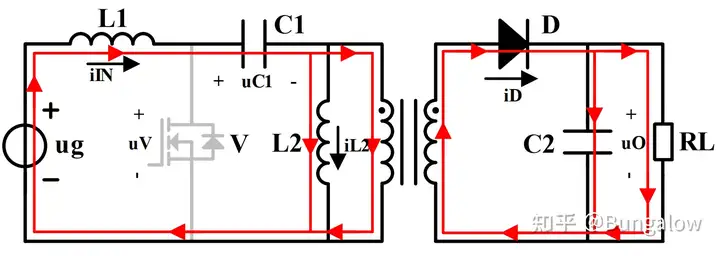
ug−uL1(off)−uC1−uL2(off)=0 (1-4)
kuL2(off)=uo (1-5)
iC1(off)=iin (1-6)
根据电感 𝐿1 , 𝐿2 的伏秒平衡可得:
uL1(off)(1−D)+uL1(on)D=0 (1-7)
uL2(off)(1−D)+uL2(on)D=0 (1-8)
其中D是占空比,即:
D=TTon=Tonfs (1-9)
其中 𝑓𝑠 是MOSFET开关频率。联立(1-1)(1-2)(1-4)(1-5)(1-7)(1-8)可得电压传递函数(电压增益)表达式:
uguo=1−DkD (1-10)
还可以得出电容 𝐶1 两端的电压(这个结果比较有趣,请读者耐心推导):
uC1=ug (1-11)
可见,CCM模式下SEPIC的电压增益仅与占空比和变压器变比有关。且随着占空比的增大,电压增益逐渐增大,理论上输出电压可以达到0和无穷大。电容 𝐶1 上的电压平均值始终与输入电压相等。
接下来计算电感电流。 这里仿照前面的方法,使用电感电流的平均值代替其瞬时值。从电路图中可以看出,𝐿1 的电流其实就是输入电流,根据输入输出功率平衡可得:
ugiin=RLuo2 (1-12)
其中, 𝑅𝐿 是负载电阻。由此可得:
iL1=iin=ugRLuo2 (1-13)
根据电容 𝐶1 的安秒平衡可得:
iC1(off)(1−D)+iC1(on)D=0 (1-14)
联立(1-3)(1-6)(1-14)得:
iL2=−Diin(1−D)=−ugRLuo2uokug=−RLkuo (1-15)
然后计算电流纹波,电流纹波可以由MOSFET开通或截止时的电流变化量表征,根据电感的特性方程:
LΔtΔiL=uL
取MOSFET开通时的电流变化量,对于 𝐿1 :
Δt=ton=fsD,uL=uL1(on)=ug
对于 𝐿2 :
$\large \Delta t=t_{on}=\frac{D}{f_s} $ ,uL=uL2(on)=−uC1=−ug
因此, 𝐿1 和 𝐿2 的电流纹波由下式给出:
∣ΔiL∣L=L1,L2=L∣uL∣Δt=LfsugD (1-16)
由(1-10)可得,在CCM模式下,满足:
D=kug+uouo (1-17)
将(1-17)代入(1-16)可得CCM模式下的电流纹波:
∣ΔiL∣L=L1,L2=Lfs(kug+uo)uguo (1-18)
可见CCM模式下,𝐿1 和 𝐿2的电流纹波大小与其电感值和MOSFET开关频率成反比,𝐿1 ,𝐿2越大,开关频率越高,电流纹波越小。下图展示了𝐿1 ,𝐿2的电流波形。方便起见, 之后的讨论中忽略正负, 认为 Δ𝑖𝐿=|Δ𝑖𝐿| 。
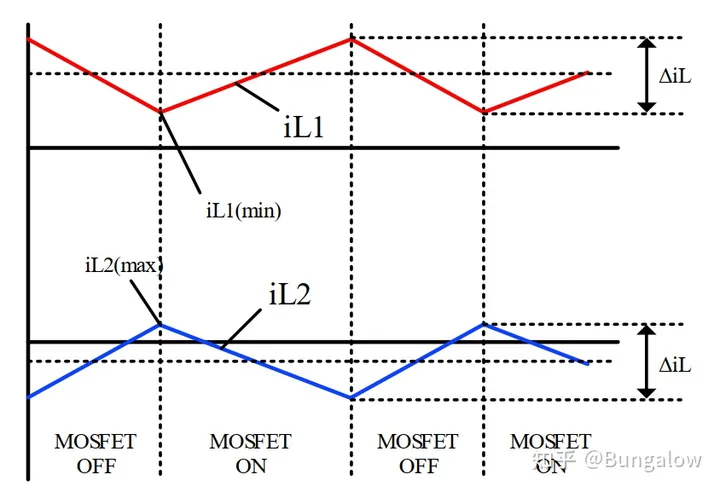
当MOSFET开通时,输入电压直接加在 𝐿1的两端, 𝐿1 被充电,所以当MOSFET截止时 𝐿1 必然放电;因为 𝐶1 两端电压为正值,当MOSFET开通时,这个电压反向加在变压器原边,副边也感应出负电压,使二极管截止,同时该电压也反向加在 𝐿2 上,使其放电,所以当MOSFET截止时, 𝐿2 必然充电。(注意这里说的充电放电是针对图中标注的电流正方向而言的)
值得注意的是,当MOSFET处于截止状态时,当 𝑖𝐿1 减小至于 𝑖𝐿2 相等时,流过变压器副边的电流降为0,二极管进入截止状态,原本建立的CCM模型失效,电路的工作状态由CCM切换至DCM(Discrete Crruent Mode)。为了防止该现象发生,需满足:
iL1(min)>iL2(max) (1-19)
因为CCM模式下两电感的电流波形为锯齿波,而由(1-13)(1-15)指出的电感电流大小实际上是电流的平均值,而对于锯齿波型而言,其平均值恰好处于两极值的中心位置,因此(1-19)可变形为:
iL1−2ΔiL1>iL2+2ΔiL2 (1-20)
将(1-13)(1-15)(1-18)代入(1-20)得:
RL<fsL1+L22L1L2(k+uguo)2 (1-21)
(1-21)展示了电路工作在CCM模式的条件,考虑到一般DC-DC的应用场景要求控制输出电压恒定,从(1-21)可以看出,在这种情况下,增大输入电压、增大负载电阻、减小开关频率和减小电感量都不利于电路工作在CCM模式。
1.2 DCM(Discrete Crruent Mode)
当(1-21)不被满足时,电路工作在DCM模式,这时,当MOSFET截止时,流过二极管的电流会逐渐耗尽,二极管最终截止,于是衍生出了SEPIC的第三个工作状态,如下图所示:
这时,由于 𝐶1 上的电压与输入电压 𝑢𝑔 相等, 𝐿1 , 𝐿2 承担的电压均为0,其电流大小均保持不变。DCM下𝐿1 , 𝐿2的电流波形如下:
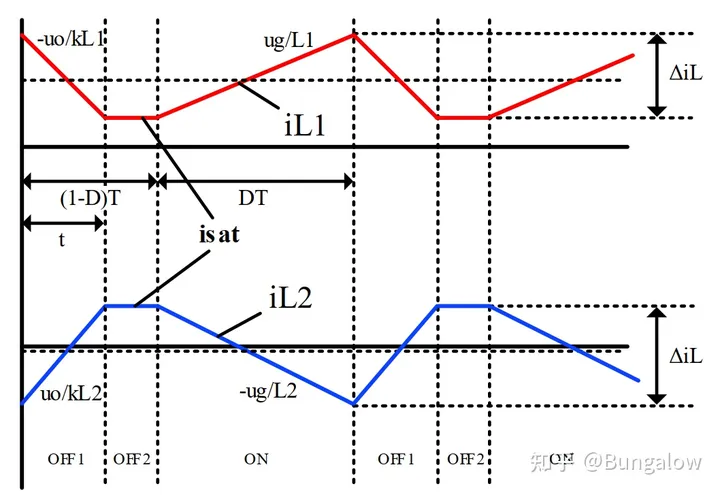
当MOSFET关断时, 𝐿1 电流减小, 𝐿2 电流先反向减小、再正向增加,设经过时间 𝑡 后, 𝐿1 电流达到其最小值,同时 𝐿2 电流达到其最大值,这时两个电感上电流达到饱和,且饱和值相等:
iL1(min)=iL2(max)=isat (1-22)
如图, MOSFET关断后经过了时间 𝑡 后 𝐿1 , 𝐿2 的电流达到饱和并相等。根据 𝐿1 , 𝐿2 充放电平衡,即MOSFET关断和开通时电感电流的变化量相等,可得:
kLuot∣L=L1,L2=ΔiL∣L=L1,L2 (1-23)
在(1-23)中,首先看等号左边的 𝑢𝑜𝑘𝐿|𝐿=𝐿1,𝐿2 ,它表示MOSFET关断时两个电感电流变化的斜率,这是怎么得出来的呢?其实,一旦电路的工作状态进入了DCM,虽然在前两个状态(图中的ON状态和OFF1状态)中(1-1)至(1-6)仍然成立,但是伏秒平衡方程(1-7)(1-8)不再成立了,然而,新的伏秒平衡方程形式与(1-7)(1-8)非常类似,我们仍然可以通过新的伏秒平衡方程得出(1-11)的结果,(这一步也交给读者去推导验证),然后我们把(1-11)代到OFF1工作状态的方程(1-4)中,再结合(1-5)就可以得到OFF1状态下的 𝑢𝐿1 和 𝑢𝐿2 ,它们都可以由 𝑢𝑜 表示,得到了电感电压,就得到了电感电流的变化率,将这个斜率乘以OFF1状态的持续时间 𝑡 ,就得到了两个电感在MOSFET关断状态下的电流变化量,也就是(1-23)中等式左边的值。
再看(1-23)的等号右边,它表示MOSFET开通时两个电感电流的变化量,尽管电路工作在DCM模式,但之前我们得到的MOSFET开通状态下的结论(1-16)仍成立,于是我们把(1-16)代入(1-23),就可以解出 𝑡 :
t=uofskugD (1-24)
接下来我们计算两个电感上电流的平均值,这里有一点需要非常注意:与CCM不同,这时的𝐿1 , 𝐿2的电流波形不再是简单的锯齿波,其平均值不能再由其极值的中点值表征,其平均值的计算方法应回归定义式,即一个周期内的积分除以时间,这里直接给出计算结果而不再展示计算步骤:
iL1=isat+2L1ugD(DT+t),T=fs1 (1-25)
iL2=isat−2L2ugD(DT+t),T=fs1 (1-26)
联立(1-25)(1-26)消去 isat ,然后就到了关键的一步。注意,(1-25)(1-26)中给出了DCM下电流平均值 iL1 , iL2的表达式,在之前讨论CCM时的(1-13)(1-15)中我们也给出了 iL1 , iL2 的表达式,其中(1-13)是由电路输入输出功率平衡得出的,所以在DCM下必然也成立;(1-15)本质上是由电容 𝐶1的安秒平衡得出的,而我们总是认为电容的电压是不会“断”的,所以在DCM下其安秒平衡方程仍然成立,所以(1-15)也成立,我们联立(1-13)(1-15),再加上 𝑡 的表达式(1-24)就可得出DCM下电压增益表达式:
uguo=D2L1L2fsRL(L1+L2) (1-27)
还可以解出 𝑖𝑠𝑎𝑡 :
isat=ugRLuo2[1−L1+L2L2(1+uokug)] (1-28)
将(1-27)代入(1-16)可得DCM下纹波电流表达式:
ΔiL∣L=L1,L2=LuoRLfs(L1+L2)2L1L2 (1-29)
1.3 总结
模式:Mode=⎩⎨⎧CCM,RL<fsL1+L22L1L2(k+uguo)2DCM,RL>fsL1+L22L1L2(k+uguo)2 (1-30)
电压增益:uguo=⎩⎨⎧1−DkD,CCMD2L1L2fsRL(L1+L2),DCM (1-31)
电流平均值:iL1=iin=ugRLuo2,CCM&DCM (1-32)
iL2=−RLkuo,CCM&DCM (1-33)
电流纹波:ΔiL∣L=L1,L2=⎩⎨⎧Lfs(kug+uo)uguo,CCMLuoRLfs(L1+L2)2L1L2,DCM (1-34)
电感 𝐿1 电流最大值:
iL1={iL1+2ΔiL1 ,CCMisat+ΔiL1,DCM (1-35)
电感 𝐿2 电流最小值(反向最大值):
∣iL2(min)∣={−iL2+2ΔiL2,CCM−isat+ΔiL2,DCM (1-36)
二.元件参数计算
2.1 MOSFET最大承受电压
只有在MOSFET截止时承受电压,这时:
uMOSFET(off)−uC1−uL2(off)=0 (2-1)
当 𝑢𝐿2(𝑜𝑓𝑓) 不为零时 𝑢𝑀𝑂𝑆𝐹𝐸𝑇(𝑜𝑓𝑓) 最大,将(1-5)(1-11)代入(2-1)可得:
uMOSFET(off)=ug+kuo (2-2)
正如前面所说的,DC-DC一般以控制 𝑢𝑜 恒定为目的,所以这里认为 𝑢𝑜 为定值而 𝑢𝑔 在一定范围内变化,可得:uMOSFET(max)=ug(max)+kuo (2-3)
注意这里 𝑢𝑜 和 𝑢𝐶1 其实是有纹波的,严格来讲应该代入其最大值计算,但是由于电压纹波一般情况下非常小,这些纹波造成的误差甚至还不如器件参数不准确造成的误差大,所以可以忽略不计。之后的推导也同样忽略电容电压纹波。
2.2 二极管最大承受电流
同样只有在MOSFET截止时二极管才可能流过电流,电流大小为:
iD=kiL1−iL2 (2-4)
在一个开关周期内,当MOSFET刚关断时, 𝑖𝐿1 有最大正值而 𝑖𝐿2 有最小负值,这时流过二极管的电流最大,为:
iD(max)=kiL1(max)+∣iL2(min)∣ (2-5)
2.3 二极管最大反向承受电压
只有在两种情况下二极管会处在截止状态,第一种情况是CCM下的MOSFET开通状态;第二种情况是DCM下的第三工作状态。在这两种情况下,对二极管两端电压进行分析,其右侧电压恒为 𝑢𝑜 ,左侧电压在这两种情况下分别为和𝑘𝑢𝐿2(𝑜𝑛) 和 0 ,将(1-2)(1-11)代入,显然前者情况下承受的电压更高,其值为:
uD(reverse)=uo+kug (2-6)
最大值为:
uD(reverse)max=uo+kugmax (2-7)
2.4 MOSFET最大正向电流
只有在MOSFET开通时其承受正向电流,这时:
iMOSFET=iL1−iL2 (2-8)
这里仿照2.2中的分析方法,可得:
iMOSFET(max)=iL1(max)+∣iL2(min)∣ (2-9)
2.5 电感选值
电感的选值的主要依据是电流纹波。假定要求额定输入和额定负载下电感纹波不超过电流均值的a(通常5%<a<40%)倍,有:
ΔiL∣L=L1,L2<aiL∣L=L1,L2 (2-10)
一般情况下当系统工作在额定状态时负载较重,处在CCM模式。
对于 𝐿1 ,将(1-13)(1-18)代入(2-10)可得:
L1>afsRLuguo(k+uguo)1 (2-11)
对于 𝐿2 ,将(1-15)(1-18)代入(2-10)可得:
L2>akfsRLk+uguo1 (2-12)
当然这里还要使用(1-21)来验证电路是否工作在CCM。





