什么是向量

前言

提到向量，高中生都知道有大小有方向的量就是向量。可是为什么要弄出这样的量呢？向量的各种计算为什么就要像课本上规定的那样呢？或许这篇文章能给你一些回答呢！走，看看去。

向量思想的萌芽

要说向量思想的萌芽，溯源可以查到上古大神亚里士多德的头上，他在著作《力学》里面有写道：“当一个物体以一定比率移动时（即含有两个有常数比率的直线运动），物体一定沿一直线运动，这条直线是由这两条有给定比率的直线形成的平行四边形的对角线。”

用现在的话说便是速度这个向量合成时满足平行四边形定则。显然这些现代的概念放在上古时代有点强人所难了，所以向量的思想也就暂时没有了后续。

平行四边形定则

时光如梭，转眼过了两千余年，时代的巨人牛顿在他的《自然科学的数学原理》里把平行四边形定则作为运动定律的一个推论叙述如下：“直接的力$𝐴𝐷$由任意倾斜的力$𝐴𝐵$和$𝐵𝐷$合成，且反过来，任意直接的力$𝐴𝐷$分解为任意倾斜的力$𝐴𝐵$和$𝐵𝐷$。的确，这种合成与分解从力学已得到了充分的证实”。然后balabala给出了一大串详细地证明，你若有兴趣，可以去原著里膜拜牛爷的智商。

尽管如此，牛顿也没有意识到自己的论证里竟然有一个重要的数学概念——向量，更没有意识到平行四边定则其实就是在作“向量的加法”运算。向量的思想虽然在物理问题里酝酿已久，但真正使得向量离开襁褓的却是看似与它毫不相关的复数！

复数是什么

复数是什么？回答这个问题得先从数是什么回答起。数其实是咱们人类创造的一个概念！我们最熟悉的1、2、3...这样的自然数便是如此。自然数可以表示物体的数量又可以表示顺序，比如你可以说“4根香蕉”、“第2个苹果”。香蕉和苹果都是真实存在的，但是数只存在于你深深的脑海里。

既然数是基于人类认识而创造的概念，那么随着认识的加深，概念的内涵也会随之延伸。于是数就慢慢变得儿孙满堂了——零、负数、分数以及无理数，以上这些都被称为实数。别看现在这些数在九年级以前都会学到，但每一种数的横空出现都伴随着认知的巨大提升。

认知被提升了一次就不愁有下一次，伴随着三次方程的求解就出现了平方后结果为负数的数！咱们都知道涉及负数的乘法规则为“正×负=负”、“负×负=正”，这意味着两个相同实数相乘的结果不可能为负数，但是这种现有认知在三次方程的解的面前破防了！

怎么办？不承认这种数吧，它却实实在在是三次方程的一个解；承认吧，它是啥呢？没错，它就是虚数！

所谓虚数就是平方后结果为负数的数，由于“正×正=正”、“负×负=正”，普通的实数当中不存在平方后结果为负数的数。于是咱们就定义这样一个数$𝑖$，其满足$𝑖^2=−1$，数$𝑖$便是虚数。

有了虚数就很容易抛出复数，因为复数就是把实数和虚数组合在一起的数。咱们给复数记作“$𝑎+𝑏𝑖$”，这里的𝑎或者𝑏都是实数，比如$2+3𝑖$或者$0.5−2𝑖$等。$𝑎$称为复数的实部，$𝑏$称为复数的虚部。

显然，如果虚部$𝑏=0$，那么复数就退化成了实数；反之实部$𝑎=0$，则复数就成了纯虚数。

虽然为了迁就三次方程的解而定义了复数，并且少数独具慧眼的数学家在解三次方程的过程中使用复数并建立了复数的运算法则，但是刚刚诞生的复数在当时并不受大部分人待见！究其原因就是人们认为虚数是一种“不存在的数”。假如能把虚数变得不“虚”，或许人们就可以接受它了。

复数的几何化

一转眼距离复数被发现已经过了两个半世纪，复数的几何化终于在韦赛尔这里实现。韦赛尔长期做着三角测量员的工作，对于如何用代数方法表示出线段的长度和方向有着强烈的愿望。于是，能力（你会怀疑韦赛尔对三角公式的了解程度吗？）与需求一碰撞，智慧的花火就出现了。

站在今天的角度来看，韦赛尔的成果仅仅是复数的入门知识，你在高中数学课本里基本可以全部学到。不过咱们要的不是现成结论，而是想知道复数是怎么和有向线段扯上关系的！来吧，接下来费点笔墨介绍介绍。

首先，韦赛尔就明确指出两条有向线段以某种方式合并即为两条有向线段相加，方法就是第二条有向线段的始端连着第一条有向线段的末端，然后由第一条有向线段始端指向第二条有向线段末端的有向线段就是两者的和。

有点绕口是不是？其实很简单，你先朝右边走了$3𝑚$得到一条有向线段，然后又往回走了$2𝑚$得到另一条有向线段，最后所得的有向线段是不是只是朝右边走了$1𝑚$的结果？

推广开来，如果你走的两段路线不重合，相当于沿三角形的一边从$𝐴$走到$𝐵$，接着沿另一边从$𝐵$走到$𝐶$，则第三条边从$𝐴$到$𝐶$就是前两者的和。

按照现在的写法，这不就是$𝐴𝐵+𝐵𝐶=𝐴𝐶$么？三角形法则或者说平行四边形法则一下子就跃然纸上啦。

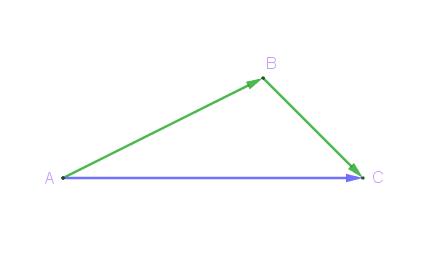
向量加法的三角形法则

接着再来看韦赛尔的一个重大创新：给出了两条有向线段乘法的几何定义，咱们来看图说话。

首先他定义了一个正单位，也就是这条有向线段的长度为1，方向沿着正方向，下图中的$𝑂𝐴$便是。

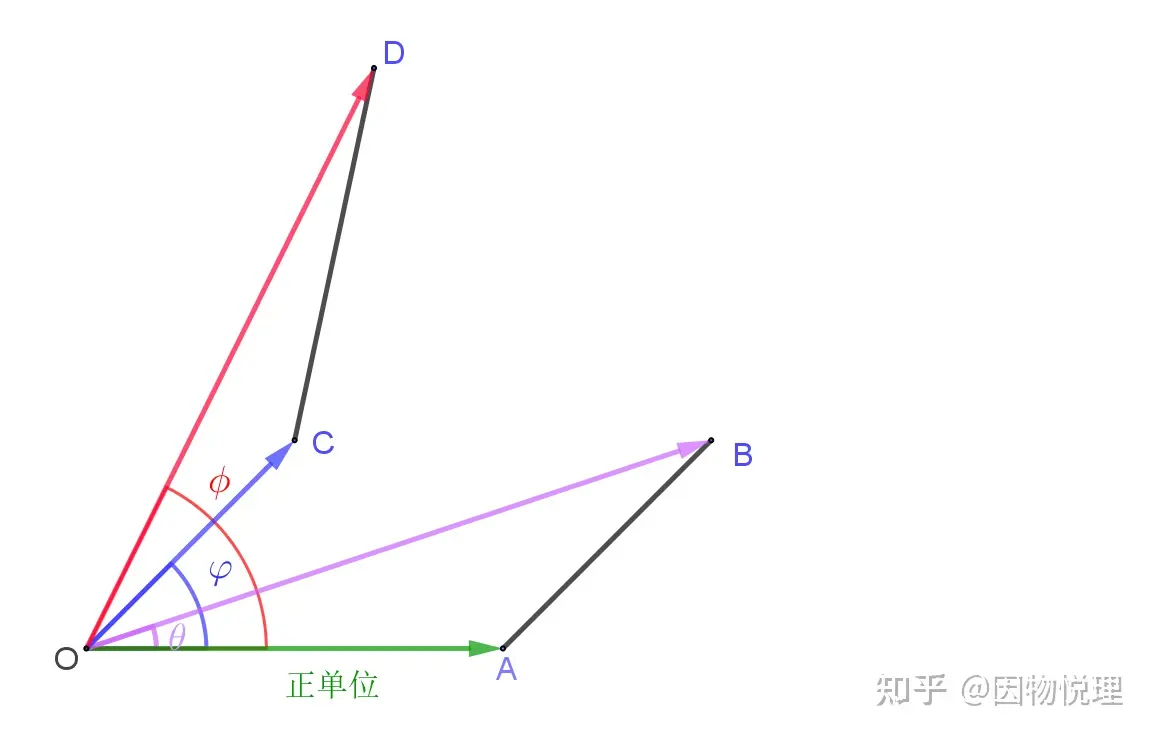
向量乘法的几何意义

然后在图中任意画出两条有向线段$𝑂𝐵$和$𝑂𝐶$，并连接$𝐴𝐵$；

最后再画出另一条有向线段$𝑂𝐷$并连接$𝐶𝐷$，使得

$Δ𝑂𝐴𝐵∼Δ𝑂𝐶𝐷$

请一定注意两个相似三角形的顶点对应关系，显然有

$∠𝐴𝑂𝐵=∠𝐶𝑂𝐷$

初中数学知识用起来哈，根据相似比就有：$𝑂𝐷=𝑂𝐵⋅𝑂𝐶$这是因为$𝑂𝐴$的长度为1，所以省略了。

你瞧这个相似比结果里不就含有两条有向线段$𝑂𝐵$和$𝑂𝐶$的长度乘积么？说明这两条有向线段的乘积大小就是有向线段$𝑂𝐷$的长度。

至于有向线段$𝑂𝐷$的方向也与$𝑂𝐵$和$𝑂𝐶$脱不了干系。

咱们用$𝑂𝐵$与正单位所成夹角（也称为方向角，下同）𝜃和$𝑂𝐶$的方向角𝜑来体现它俩各自的方向，由于存在$∠𝐴𝑂𝐵=∠𝐶𝑂𝐷$，你是不是可以立马看出$𝑂𝐷$的方向角𝜙与𝜃和𝜑的关系？显然有

𝜙=𝜑+𝜃

看完以上部分，你意识到什么没有？明确了有向线段的加法与乘法的几何意义后，咱们就可以利用事先已知的两条有向线段去得出一条新的有向线段！并且只需要利用少许的代数计算就能完成！这不正是韦赛尔的初衷么？

这还没完，真正要使这个想法能付诸实际，还需他迈出非凡的一步。

实数计算的结果只有正负之分，正的结果表示和正单位同向，负的结果表示和正单位反向；如此一来，方向始终不能脱离正单位所在的直线！于是韦赛尔又引进了一个𝜀，用来表示垂直正单位且原点相同的单位。

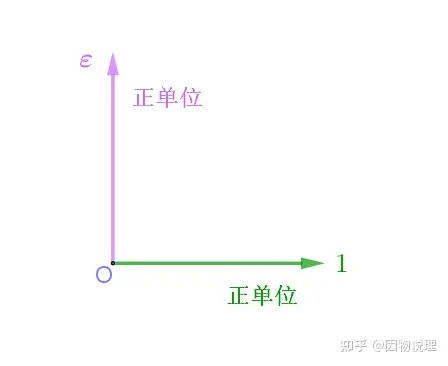
引入另一个正单位后使得复数的可视化得以实现

如此一来，+1的方向角为0∘，−1的方向角为180∘，𝜀的方向角为90∘，−𝜀的方向角为270∘。

刚才咱们不是得到了有向线段乘积的方向角等于这两条有向线段方向角的和么？咱们立刻就能写出如下一些式子：

$(+1)(+1)=+1；$

$(+1)(−1)=−1；$

$(−1)(−1)=+1；$

(+1)(+𝜀)=+𝜀；

(+1)(−𝜀)=−𝜀；

(−1)(+𝜀)=−𝜀；

(−1)(−𝜀)=+𝜀；

(+𝜀)(+𝜀)=−1；

(+𝜀)(−𝜀)=+1；

(−𝜀)(−𝜀)=−1。

请不要不稀罕这些式子！你把每个式子里的括号都看成是一个有向线段，乘积的结果也看成有向线段，那么上述式子很自然地就成立了。

你瞧嘛，有向线段乘以−1的结果就是将其旋转180∘；有向线段乘以𝜀的结果就是将其旋转90∘。其它的式子就留给你自己去体会其中的几何奥秘了哈。

哈哈哈，新引进一个正单位𝜀后，不仅能和普通的乘法运算和平相处（抛开最后三个等式，你看看是不是都满足“正负得负，负负得正”？），而且还必然得出（最后三个等式）𝜀^2等于$−1$。这不正是前面已经出场的虚数$𝑖$么？到此，虚数$𝑖$也就有了确定的几何意义！

说完了虚数，就该轮到复数啦。按照韦赛尔已经提出的有向线段的加法法则，长度为1的某条有向线段$𝑂𝑃$可以写成（见下图）$𝑂𝑃=𝑂𝑀+𝑀𝑃$

如果把$𝑂𝑃$的方向角记为𝜔，则$𝑂𝑀$的长度为𝑂𝑀=cos⁡𝜔，而𝑀𝑃的长度为𝑀𝑃=sin⁡𝜔。

随着𝜔在一周内任意取值，cos⁡𝜔和sin⁡𝜔都会出现正值与负值。cos⁡𝜔有正负正好可以体现出$𝑂𝑀$的方向，因为$𝑂𝑀$始终与正单位+1在一条线上，不是与+1同向就是与−1同向，所以cos⁡𝜔把𝑂𝑀的长度与方向一起抓了！

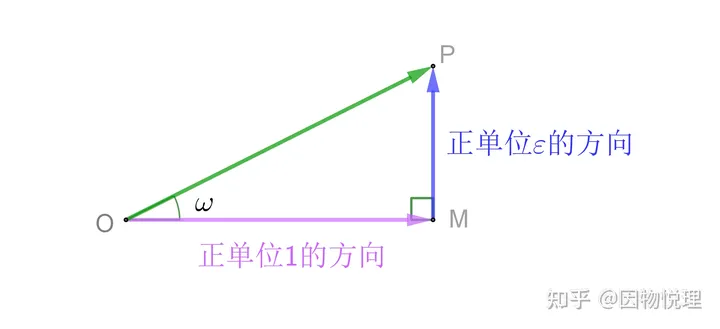
复数加法的几何意义

但是sin⁡𝜔的正负咋解释咧？正负是正单位+1这条线上的两个专属方向，你$𝑀𝑃$的方向是与另一个正单位𝜀的方向相同或者相反的，你别在正单位+1这条线上凑热闹撒！

所以为了同时表示𝑀𝑃的长度和方向，咱们必须要写成𝑀𝑃=𝜀sin⁡𝜔。这样一来，sin⁡𝜔的正负就体现为是+𝜀还是−𝜀，这不就完美体现出了𝑀𝑃的方向么？

于是你就会看到长度为1的某条有向线段$𝑂𝑃$可以被表示为𝑂𝑃=cos⁡𝜔+𝜀sin⁡𝜔

你把𝜀换成虚数$𝑖$不就是现在高中数学课本里所写的结果么？而这个结果是啥？妥妥滴的复数呀！

如果你再把有向线段的长度变为$𝑟$，$𝑟$既可以大于1也可以小于1，则该条有向线段就能表示为𝑟(cos⁡𝜔+𝑖sin⁡𝜔)

由此，平面上任何一条有向线段都有一个复数和它如影随形，并且复数的运算规则也都能用有向线段的各种变化加以说明，这才有了如今你在数学课里所学到复数知识。复数的几何解释完美收官！

这份创造性的成果后经高斯等人站台得到了彻底推广与认可，复数终于有了自己的合法地位，不再是数系大家庭里的一名“黑户”。

不过美中不足的是，复数的这种几何表示只能处理平面上的向量。因为咱们只是建立了一个平面直角坐标系，按现在的术语来说，正单位+1所在的轴称为实轴，正单位$+𝑖$所在的轴称为虚轴；

在这个坐标系里任取一点$𝑄$记作$(𝑥,𝑦)$，则有向线段$𝑂𝑄$也被记作$(𝑥,𝑦)$；而$𝑂$点和$𝑄$都在这个坐标系的平面里，所以有向线段$𝑂𝑄$也就没法脱离坐标系所在的平面。

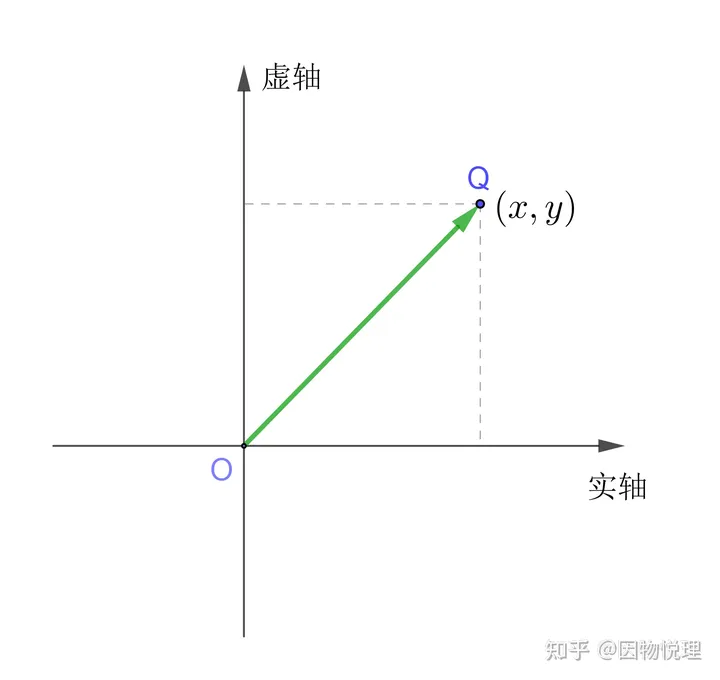
平面向量与复数的对应关系

如此一来，面对存在于空间里的有向线段就得吃瘪了。于是乎，推广复数使其能表示空间有向线段的动机就很明显了。

没办法，人一吃饱了就喜欢多想。把这股子劲使在科学研究上是极好不过了，现在又该轮到谁出来搞事情了呢？（友情提示：吃饱了可不能干坏事，这是犯法的！你知道不？）

哈密顿的四元数

大神哈密顿（没错，就是这篇文章里的主角之一）此时又云淡风轻地站了出来，表示对上述问题很感兴趣。不过他的出发点是想把复数推广成三维空间的数。

此话怎讲？你知道有数轴这么一个好用的工具吧？每个实数都在数轴有唯一的点与之对应，这便是实数的几何解释。

由于数轴只是一条线，所以咱们可是说实数一维空间的数。而复数的几何表示需要用到平面坐标系，所以说复数是二维空间的数。

数轴可以表示出一切实数

如今既然是将复数推广成三维空间的数，那么推广的复数自然就得写成$𝑎+𝑏𝑖+𝑐𝑗$的形式，这里的$𝑗$和$𝑖$一样，也有$𝑗^2=−1$。

由于有三项相加，所以推广之后的数被冠名为三元数。说实话，就这种推广方式估计你我都能想到，不过这么推广会不会有啥问题，还得由高人才能看得出来。哈密顿为此可是煞费了一番苦心！

如此推广的复数，问题出在了三元数的乘积上。两个复数进行加、减、乘、除，其结果依然是复数，自己去翻看高中数学教材来一波回忆杀。但是两个三元数相乘之后，结果就有点尴尬了。

对于两个三元数的乘积

$(𝑎_0+𝑎_1𝑖+𝑎_2𝑗)(𝑏_0+𝑏_1𝑖+𝑏_2𝑗)$

按照复数的乘法规则打开括号，并且利用

$𝑖^2=𝑗^2=−1$

的特点就能得到结果。

最后化简的结果我就直接放出来，为：

$(𝑎_0𝑏_0−𝑎_1𝑏_1−𝑎_2𝑏_2)+(𝑎_0𝑏_1+𝑎_1𝑏_0)𝑖+(𝑎_0𝑏_2+𝑎_2𝑏_0)𝑗+𝑎_1𝑏_2𝑖𝑗+𝑎_2𝑏_1𝑗𝑖$

各位请自行验证。

眼瞅着结果里的前三项是三元数，可是添上最后两项就变得不伦不类了。怎么处理$𝑖𝑗$或者$𝑗𝑖$困扰了哈密顿十来年的时间——因为这种情况里，只有令$𝑖𝑗=𝑗𝑖=0$才能确保两个三元数的乘积依然是三元数，但是这样又会出现另一个矛盾。走，看看去。

对于复数$𝑧=𝑎+𝑏𝑖$来说，复数的模或者说表示复数的有向线段的长度为:

$|𝑧|=\sqrt{𝑎^2+𝑏^2}$

复数的模有这么一个特点——若两个复数的乘积记为:

$(𝑎_1+𝑏_1𝑖)(𝑎_2+𝑏_2𝑖)=𝑎_3+𝑏_3𝑖$

则有

$(𝑎_1^2+𝑏_1^2)(𝑎_2^2+𝑏_2^2)=𝑎_3^2+𝑏_3^2$

即两个复数模的乘积等于这两个复数乘积的模，你可以利用复数乘法规则去验证一下。

哈密顿当然希望三元数的模也有这样的特点。但是你去验证之后就会发现上面所得的两个三元数的乘积结果里，要是令$𝑖𝑗=𝑗𝑖=0$，则必然会导致

$(𝑎_0^2+𝑎_1^2+𝑎_2^2)(𝑏_0^2+𝑏_1^2+𝑏_2^2)≠(𝑎_0𝑏_0−𝑎_1𝑏_1−𝑎_2𝑏_2)^2+(𝑎_0𝑏_1+𝑎_1𝑏_0)^2+(𝑎_0𝑏_2+𝑎_2𝑏_0)^2$

也就是说模的特点不满足。

不过哈密顿发现，要是令$𝑖𝑗=−𝑗𝑖$，则三元数的模的特点就能得以满足，但是这会导致两个不同三元数的乘积就不是三元数了。

需要提醒你的是这里有个特例，要是两个三元数相同，即$𝑎_0=𝑏_0、𝑎_1=𝑏_1、𝑎_2=𝑏_2$，则在$𝑖𝑗=−𝑗𝑖$的条件下，其乘积就可以变为三元数。此结论留给你去验证哈。

总之，显而易见推广而来的三元数在解决$𝑖𝑗$这一项时遇到了不可调和的矛盾！要说如何破局，经过十多年的探索，哈密顿终于意识（真的算是长期思考后的灵光一现，于散步的时候想出了解决办法）到还需要加一个分量$𝑘$，使得$𝑖𝑗$等于这个未知分量。

由于多了一个分量，那么三个分量之间就会两两组合，所以还需满足$𝑖𝑗=−𝑗𝑖=𝑘，𝑗𝑘=−𝑘𝑗=𝑖，𝑘𝑖=−𝑖𝑘=𝑗$。同时，这里新增的分量$𝑘$和分量$𝑖、𝑗$一样都满足

$𝑖^2=𝑗^2=𝑘^2=−1$

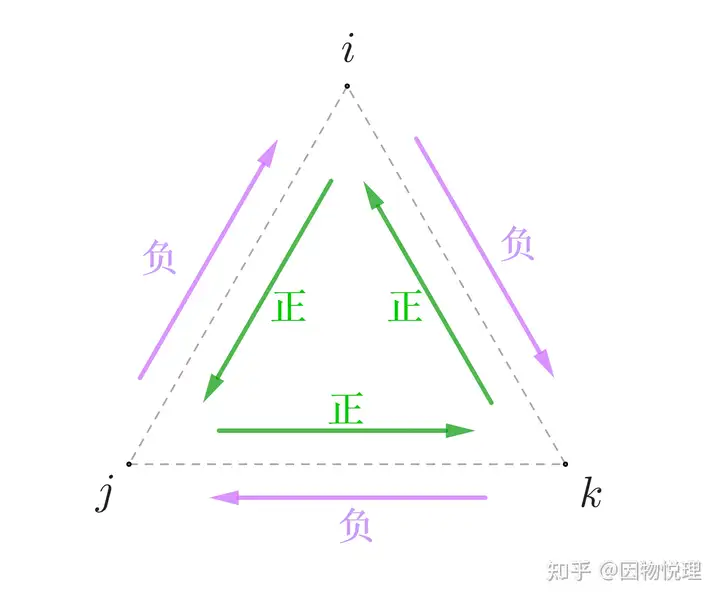
说明：按图中绿色箭头的顺序（字母的字典顺序）任取两个分量求乘积，结果等于第三个分量；若按图中紫色箭头的顺序任取两个分量求乘积，结果等于第三个分量的相反数。

经过这样的处理之后，哈密顿推广的新数就能满足复数的所有特点！不过需要指出的是新数并不满足乘法的交换律性质，这是由各个分量之间的特点所决定的——因为

$𝑖𝑗≠𝑗𝑖，𝑗𝑘≠𝑘𝑗，𝑘𝑖≠𝑖𝑘$。

于是乎，哈密顿正式给这种新数上户口为四元数，记作

$𝑎+𝑏𝑖+𝑐𝑗+𝑑𝑘$，其中$𝑎,𝑏,𝑐,𝑑$都是实数。

同时，哈密顿给出了四元数的一系列解释：四元数分为两个部分，第一部分𝑎只含有实数，因此被哈密顿称为纯量或者标量；第二部分就是整个虚数部分$𝑏𝑖+𝑐𝑗+𝑑𝑘$，被哈密顿首次称为向量，即此部分可以用一个有向线段来表示。

这个很好理解，若将三个分量$𝑖、𝑗、𝑘$分别看成是空间直角坐标系的三个正单位轴，那么虚数部分不就可以表示成$(𝑏,𝑐,𝑑)$了么？你看，空间里的有向线段不就再次和复数牵手了嘛？！

终于，向量这个词在哈密顿这里诞生了，往后经过数学家们的抽象而有了严格的定义。简要地说就是有一个集体满足一定的运算规则，那么这个集体里面的任意一个元素就是一个向量。

打个比方，比如咱们定义能直立行走的灵长类动物类群体为人类，那么这个类别里的每一位就是一个人！

向量的这种定义非常数学化，把严谨性和包容性两手一起抓了。严谨性就不说了，数学不严谨就不叫数学了；包容性是说这种数学化的定义方式占据统领地位，比如咱们常说“有大小、有方向的量是向量”也是向量的一种直观定义，这种定义方式能被证明归属于上面那种抽象的数学定义。

总而言之，向量可以有不同的定义方式，但是均殊途同归！鉴于这篇文章是为后续的物理问题服务的，这种纯数学问题咱们就别自讨没趣啦。接下来的重点是关注向量的一些具体计算。

向量的乘法

提及向量的乘法，高中生所能接触到的只有两类：一种是将一个实数与一个向量相乘，称为向量的数乘；另一种是将两个向量相乘，其乘号写成“⋅”号，称为向量的数量积或者内积。

至于为啥要弄出这么多运算规则，归根结底是由四元数之间的乘法结果所决定的。意不意外？惊不惊喜？那就看看去呗。

咱们把两个四元数分别记为

$𝐴=𝑎_0+𝑎_1𝑖+𝑎_2𝑗+𝑎_3𝑘$

和

$𝐵=𝑏_0+𝑏_1𝑖+𝑏_2𝑗+𝑏_3𝑘$则两者的乘法结果为：

$𝐴𝐵=(𝑎_0𝑏_0−𝑎_1𝑏_1−𝑎_2𝑏_2−𝑎_3𝑏_3) +(𝑎_0𝑏_1+𝑎_1𝑏_0)𝑖+(𝑎_0𝑏_2+𝑎_2𝑏_0)𝑗+(𝑎_0𝑏_3+𝑎_3𝑏_0)𝑘 +(𝑎_1𝑏_2−𝑎_2𝑏_1)𝑖𝑗+(𝑎_2𝑏_3−𝑎_3𝑏_2)𝑗𝑘+(𝑎_3𝑏_1−𝑎_1𝑏_3)𝑘𝑖$

各位不要被劝退了，你就当是两个普通的四项式相乘，结果是不是得有十六项？你挨个数数上面的项数就知道了。

至于合并的结果里，无非是用到了四元数里三个虚数分量的特点：即

$𝑖^2=𝑗^2=𝑘^2=−1$和$𝑖𝑗=−𝑗𝑖=𝑘，𝑗𝑘=−𝑘𝑗=𝑖，𝑘𝑖=−𝑖𝑘=𝑗$。

只提醒各位一点，四元数的乘法不满足交换律，所以$𝐴𝐵$与$𝐵𝐴$的结果不要弄混了哟。另外呢，我特意没有把$𝑖𝑗$项、$𝑗𝑘$项和$𝑘𝑖$项替换成$𝑘、𝑖$和$𝑗$，目的有俩：一来能直接反映出相乘的结果；二来还有更深的内幕可挖。

说实话，谁看见这十六项结果不烦呢？所以很有必要引入几个符号来简化结果。

按照哈密顿对四元数的解释——分为标量部分和向量部分，那么咱们就把四元数的向量部分用加粗斜体字母来表示，这和如今数学教材里的表示方法一致。则前述的两个四元数可以记为

$𝐴=𝑎_0+\alpha$和$𝐵=𝑏_0+\beta$。

然后我们把

$𝑎_1𝑏_1+𝑎_2𝑏_2+𝑎_3𝑏_3$记作$\mathbf{\alpha}⋅\beta$。

把上述乘积结果的最后三项

$(𝑎_1𝑏_2−𝑎_2𝑏_1)𝑖𝑗+(𝑎_2𝑏_3−𝑎_3𝑏_2)𝑗𝑘+(𝑎_3𝑏_1−𝑎_1𝑏_3)𝑘𝑖$ 记作 $\alpha×\beta$

而上述乘积结果的中间三项可以改写成

$𝑎_0(𝑏_1𝑖+𝑏_2𝑗+𝑏_3𝑘)+𝑏_0(𝑎_1𝑖+𝑎_2𝑗+𝑎_3𝑘)$则可记作$𝑎_0\mathbf{\beta}+𝑏_0\alpha$

你瞧，向量的数乘$𝑎_0\mathbf{\beta}与𝑏_0\alpha$ 、向量的数量积$\mathbf{\alpha⋅\beta}$不就都有着落了么？

显然向量数乘的结果依旧是向量，而向量数量积的结果却是一个标量。

至于$\alpha×\beta$是向量的另外一种乘法，称为向量的外积，与向量的内积加以区分，其结果依旧是一个向量。

你问我为啥这么定义，难道弄出这么几个简单的记号去替代那十六项结果不香吗？谁愿意把自己的名字取得超级长？这怕是考试的时候写名字没吃过亏吧？

有了这几个记号，那么先前两个四元数的乘积就可以写成

$𝐴𝐵=(𝑎_0𝑏_0−\alpha⋅\beta)+(𝑎_0\beta+b_0\alpha)+\alpha \times\beta$

你看嘛，整个世界不就清爽了嘛？！根据记号的特点，咱们可以很容易看出乘积结果里的第一项是标量部分、而后两项都是向量部分。

要是把四元数“阉割”一下，令两个四元数的标量部分都为零，即$𝑎_0=0$且$𝑏_0=0$，那么四元数就只含有向量部分，即

$𝐴=𝑎_1𝑖+𝑎_2𝑗+𝑎_3𝑘$和$𝐵=𝑏_1𝑖+𝑏_2𝑗+𝑏_3𝑘$

来来来，自己动手算一算这两个四元数的乘积吧，有

$𝐴𝐵=−\alpha⋅\beta+\alpha×\beta$

请记住这个等式，它在后面可是大有作为的哟！

对了，作为哈密顿忠实粉丝的泰特在推广四元数的过程里发现了很多结论，其中就有

$\alpha⋅\beta=\alpha\beta cos\theta$和$\alpha×\beta=\alpha\beta sin\theta\widehat{n}$

等式里的𝜃是向量$\alpha$和$\beta$之间的夹角，而$\widehat{n}$是垂直于向量$\alpha$和$\beta$的单位向量，可用右手螺旋定则来确定$\widehat{n}$的方向。

这两个结论不是这里的重点，甩出来就行了。如此一来，计算向量乘法的代数方法和几何方法就齐活啦。

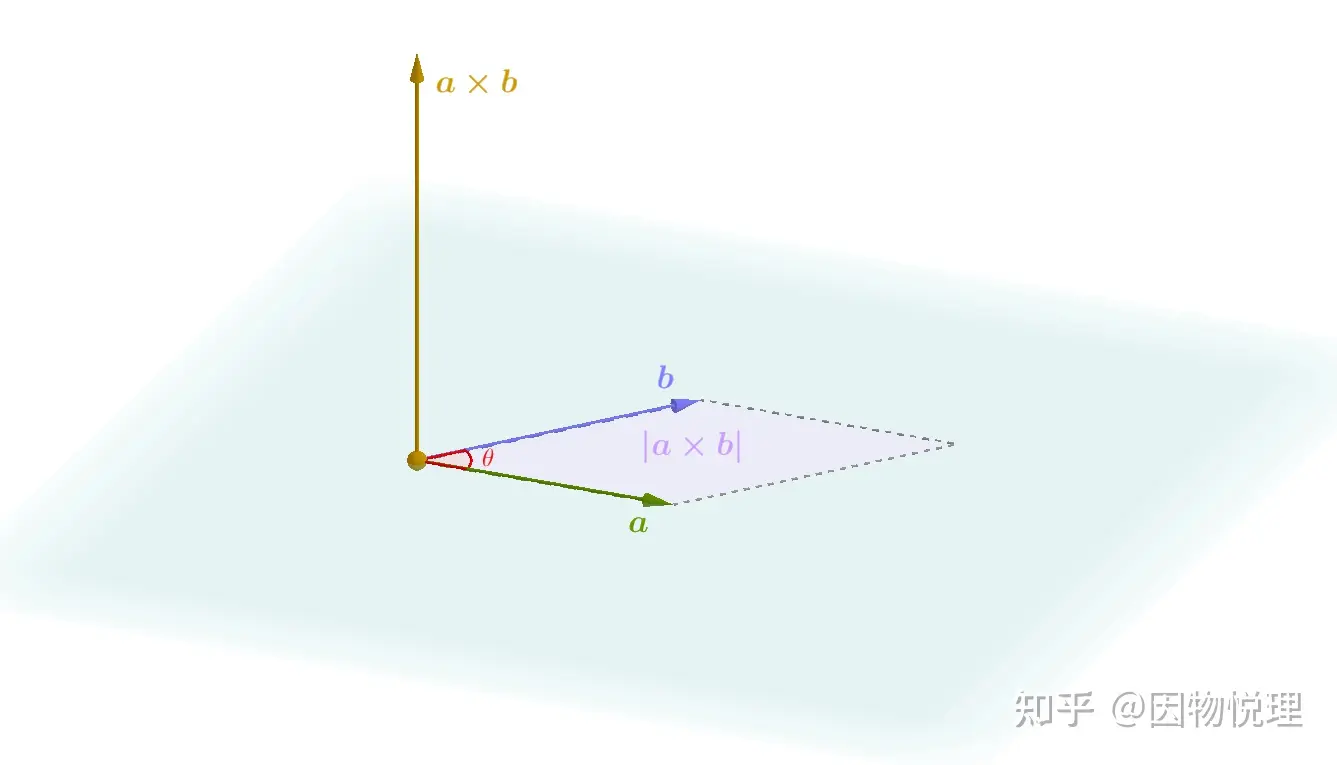
立体图：向量叉乘的几何意义

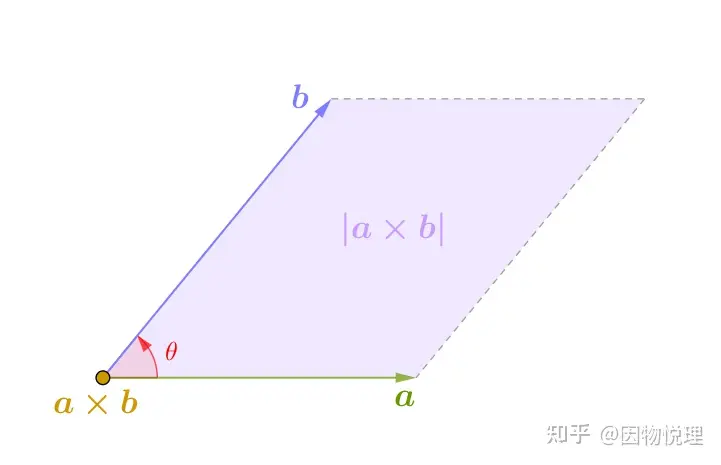
俯视图：向量叉乘与向量点乘的几何意义。此图很明显反映出了右手螺旋规则——四值绕向与图中夹角方向一致，大拇指的指向即为图中黄点的方向（垂直纸面向外）

“▽”算子来啦

刚才之所以提到“阉割”版四元数，这是因为四元数恰好诞生在电磁学飞速发展的时期，而描述电磁现象的物理量大都是向量，为了更加方便地对向量进行运算，就没有必要去使用完全版的四元数，于是在精简版四元数基础上应运而生了向量分析。

提到向量分析，怎能少了大名鼎鼎的“∇算子”呢？欢迎登场！

“∇算子”最早由哈密顿作为一个简化的记号开始使用，他定义

$∇=𝑖\frac{∂}{∂𝑥}+𝑗\frac{∂}{∂𝑦}+𝑘\frac{∂}{∂𝑧}$

都说了是一个简化记号，你也就不用去纠结为啥这么干了。你可以把“∇算子”看成是一个“阉割”版的“四元数”或者是一个“空间向量”。

你是否好奇为啥“四元数”和“空间向量”都要加上引号呢？

原因在于“∇算子”里各个虚数分量的系数都是待定的偏导符号，如果这些偏导符号不作用于一个具体的量何来确定的值呢？没有具体的值，你怎么能说“∇算子”是一个四元数或者空间向量呢？

所以当“∇算子”单独出现的时候，它只是一个孤独的记号罢了。不过就冲它这长相，确实和“阉割”版四元数或者空间向量的表示方法很像！

想不想看看“∇算子”怎样用呢？

很简单，你把它“当做”普通向量，于是它可以作用于一个标量𝑑，则有

$∇=𝑖\frac{∂d}{∂𝑥}+𝑗\frac{∂d}{∂𝑦}+𝑘\frac{∂d}{∂𝑧}$

一个向量与标量相乘不就是向量的数乘么？所以∇𝑑是一个向量没毛病。

既然在用“∇算子”时将其“当做”普通向量，它当然可以和另一个向量$𝐷$进行乘法撒。

按照空间向量的表示方法，向量$𝐷$被记为$𝐷=𝑖𝐷_𝑥+𝑗𝐷_𝑦+𝑘𝐷_𝑧$

这不立刻就有

$∇\cdot D=𝑖\frac{∂D_x}{∂𝑥}+𝑗\frac{∂D_y}{∂𝑦}+𝑘\frac{∂D_z}{∂𝑧}$

么？

妥妥的就是向量的数量积嘛！结果是标量，也没毛病。至于$∇×𝐷$的结果就留给你自己去展开了哈。照抄向量外积的答案即可。

尽兴了没？要不再来看几个“∇算子”的有趣操作呗。

如果把两个“∇算子”放一起进行四元数乘法，会擦出啥火花呢？老规矩，按照四元数乘法规则，两个纯向量部分的结果为：

$∇∇=−∇⋅∇+∇×∇$

而

$∇⋅∇=\frac{∂^2}{∂𝑥^2}+\frac{∂^2}{∂𝑦^2}+\frac{∂^2}{∂𝑧^2}$

$∇×∇=(𝑖𝑗+𝑗𝑖)\frac{∂^2}{∂𝑥∂𝑦}+(𝑗𝑘+𝑘𝑗)\frac{∂^2}{∂𝑦∂𝑧}+(𝑘𝑖+𝑖𝑘)\frac{∂^2}{∂𝑥∂𝑧}$

这两个结果请自觉推导哈。 显然其向量部分的

$∇×∇=0$

而标量部分被记作

$∇⋅∇=∇^2$

于是

$∇∇=−∇⋅∇=−∇^2$

别小看$∇^2$这个符号，人家也有个如雷贯耳的名字——拉普拉斯算子！不过你看计算结果的话，它其实就是个二阶偏导算符。

有没有三个四元数（其中包含“$∇$算子”）相乘的例子呢？有，这就安排上（感觉有点不可控了......）！

比如两个“$∇$算子”和一个标量相乘，即$∇∇𝑓$。按照乘法的结合律，把前面两个“$∇$算子”先做乘法运算，则有

$∇∇𝑓=−∇^2𝑓$

若先将后面两项做乘法运算，则有

$∇∇𝑓=∇(∇𝑓)=−∇⋅∇𝑓+∇×∇𝑓=−∇^2𝑓+∇×∇𝑓$

请注意，第二个等号成立是因为咱们直接应用了两个四元数纯量部分的乘法结论。

对比就能发现第一种计算方式的结果里只有标量部分$−∇^2𝑓$；而第二种计算方式里即有标量部分$−∇^2𝑓$还有向量部分$∇×∇𝑓$。

由于两种计算方式的结果必然相同，所以第二种计算方式里得到的向量部分应该为零，即$∇×∇𝑓=0$

这也意味着$∇∇𝑓$的结果是一个标量。

再看看两个“$∇$算子”和一个向量相乘，即$∇∇𝑉$。

同样的办法，先结合前面两个“$∇$算子”做乘法运算，则有

$∇∇𝑉=−∇^2𝑉$

虽然拉普拉斯算子是个标量算子，但是它作用在向量身上时，其结果依旧是向量（此处就不展开详说了）！若先将后两项做乘法运算，则有$∇∇𝑉=∇(−∇⋅𝑉+∇×𝑉)=−∇(∇⋅𝑉)+∇(∇×𝑉)$

第一个等号成立是因为再次用到了两个四元数纯量部分的乘法结论。

上面等式最右边的第二项是“$∇$算子”与向量（$∇×𝑉$的结果是向量）的相乘，所以又可以套娃应用四元数纯量部分的乘法结论，则有结果

$∇(∇×𝑉)=−∇⋅(∇×𝑉)+∇×(∇×𝑉)$

所以按照第二种计算方式得到的结果为：

$∇∇𝑉=−∇(∇⋅𝑉)−∇⋅(∇×𝑉)+∇×(∇×𝑉)$

你能瞅出这个结果里，哪些是向量部分、哪些事标量部分吗？

没错，只有第二项$∇⋅(∇×𝑉)$是标量，其余两项是向量。对比两种计算方法所得的结果，必然有标量部分

$∇⋅(∇×𝑉)=0$

且向量部分存在关系

$−∇(∇⋅𝑉)+∇×(∇×𝑉)=−∇^2𝑉$

移项之后便能得到一个非常有用的结论

$∇×(∇×𝑉)=∇(∇⋅𝑉)−∇^2𝑉$

敲黑板，后面的物理文章会用到哟！

好啦，就此打住，再写下去就真的没完没了了，毕竟以上写出的东西在后续的物理文章中已经够用了。

其实你在电动力学的教材里都能找到比上述更多的结论，不过我在这里依旧花了一些笔墨来介绍部分结论，其原因就是希望你清楚地知道它们都是通过四元数的基本运算规律而来，这样你就不至于在看到它们的时候一脸懵圈。

真正让“∇算子”发挥实际作用的大神还得看麦克斯韦！他在统一电磁理论的过程里，法拉第提出的场的观点可谓是深入他心。为了形象描述场的特点，法拉第创造了力线（按现在的叫法应该是电场线与磁感线）这样假想的工具，想必大伙都知道这些史实。

那么麦克斯韦面临的问题就是如何把这些工具精确地数学化。在这个过程里，麦克斯韦与“$∇$算子”结下了不解之缘，$∇⋅𝐷$、$∇×𝐷$还有$∇𝑑$都各自拥有了自己的户口，分别是向量𝐷的散度、向量𝐷的旋度和标量𝑑的梯度。

对了，刚才得到的结论里，

$∇×∇𝑓=0$

即标量𝑓的梯度的旋度等于零

与

$∇⋅(∇×𝑉)=0$

即向量𝑉的旋度的散度等于零都是恒成立的结论，于是你可以记下口诀“梯无旋、旋无散、姬无命”。

是不是觉得这三个名称都怪里怪气的？其实不是名称怪，而是你不明白为啥把这些名称扔给这些记号。深吸一口气，咱这就来说说散度、旋度和梯度的来历！

向量场的散度

要把法拉第提出的力线工具数学化，麦克斯韦最终将目光停留在了流体身上。因为他发现力线与不可压缩的流体的流线有很多相似，于是描述流体的数学框架就被他移植到了统一电磁场理论的工作中去。类比方法被他玩得溜起！

这里需要先简单聊一聊两个词语，先说流体的流线。比如说在管道中流动的水，咱们就很关心管道里各处的水流速度大小和方向。

为了便于进行数学描述，咱们会把管道各处的水流速度大小和方向用一个有向箭头给表示出来：箭头方向代表该处的流速方向、箭头长度表示该处的流速大小。

但是你没有必要把每个点处的速度箭头都画出来吧？看起来太凌乱了不是？于是咱们只需画出这样的曲线，在它上面的每一点处，曲线都和对应于该点的速度向量相切即可，这样的曲线就被称为流体的流线。

你瞧，用它表示水流是不是即简洁而又一目了然呢？

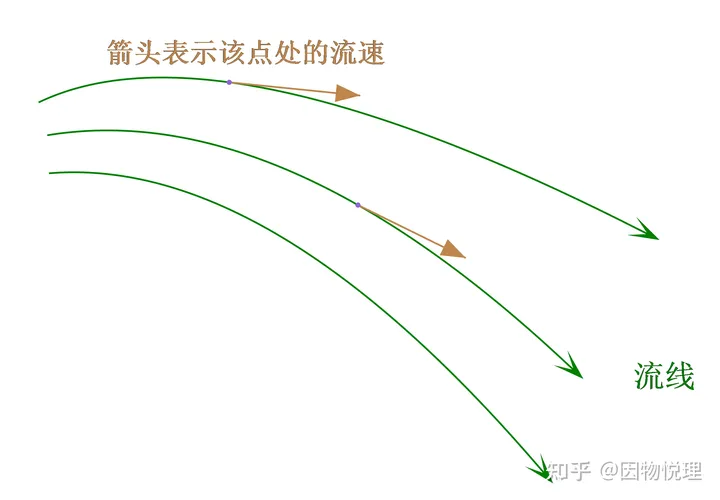
流线示意图

再来说向量场，这本是一个数学概念，这里通俗地给你解释解释。显然刚才用来表示流速的箭头是个向量，由于管道里每个地方都可以画出这样的箭头来表示速度向量，所以咱们就说管道区域里有一个向量场。

这个“场”字表示一个场所，也就是此处的管道区域。要是咱们关注的是这个区域里每一点的水温，由于温度是标量，所以咱们就该说这个区域里有一个标量场。

也就是说在咱们所关注的某个区域里，如果区域各处都存在一个向量，则该区域就是向量场；如果区域各处都存在一个标量，则该区域就是标量场。

打个比方，你在一块地里种菜，是不是该管这块地叫菜地？你要是在这块地上铺上草皮，是不是就得改口叫草坪了？

好啦，回到流体的描述里来，有一个重要的概念就是流体的流量。对于不可压缩的流体来说，有一种很简单但是又很重要的情形需要研究：管道某个区域里的流体质量不随时间的演变而变化。

通俗点说就是有个水池，上面的水龙头在往里注水，池底的排水孔在向外排水，但是在这个动态变化的过程里，池中的水量保持不变。

哈哈哈，这是不是让你想起了小学数学里放水与注水的应用题？能出现这种动态平衡的条件就是进水口的流量等于出水口的流量，所以流量对于流体来说是个非常重要的概念。

顾名思义，流量就是流体在单位时间里通过管道某一横截面积的质量。假设流体各处的流速相同且恒为𝑣，按照下图所标字母可知流体通过垂直截面的流量为

$Q = \frac{{\rho v\Delta t{S_ \bot }}}{{\Delta t}} = \rho v{S_ \bot }\\$

而通过倾斜截面的流量也为

$Q = \frac{{\rho v\Delta t{S_ \bot }}}{{\Delta t}} = \rho v{S_ \bot }\\$

毕竟同一根管道同一个梦想，不能说你弄一个倾斜截面就把流量给弄大了。

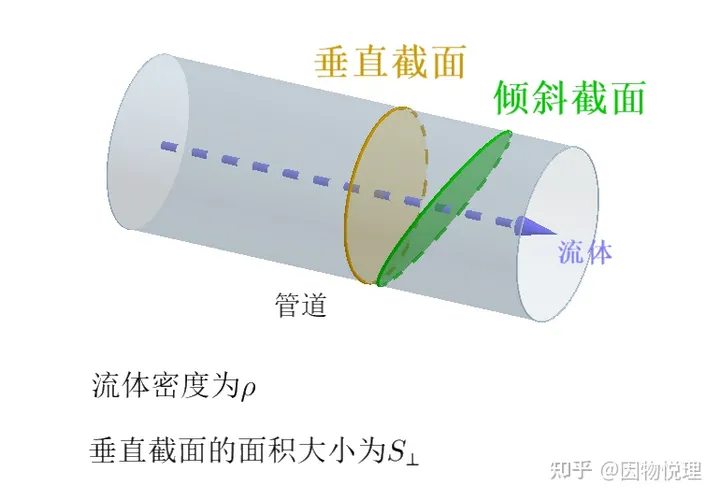
截面与通量的关系

这意味着咱们在计算流量时，选取的截面应该要与流速垂直！或者说给截面标出一个法向（即与截面垂直的方向），假若流速方向与截面法向的夹角为𝜃，则流量可以写成$Q = \rho vScos \theta \\$这里的𝑆记为任一截面的面积大小。

显然这个结果可以写成流速向量$𝑣$与截面向量$𝑆$的数量积，即$Q = \rho {\bf{v}} \cdot {\bf{S}}\\$

另外，考虑到不可压缩的流体的密度$\rho$是个常数，所以为了方便起见，咱们一般就取流体密度$\rho = 1$，则流体的流量就简化成$Q = \rho {\bf{v}} \cdot {\bf{S}}\\$

刚才得到如此简单的式子是假设了流体各处的流速相同，更一般的情形里流速哪有这么听话的？面对流体各处流速不一样的情形时，该如何求出流体通过某个截面的流量呢？

你若看过我上一篇关于微积分的文章，想必就能很快给出答案——先求出每一小块截面上的流体流量，然后把所有小截面的流量相加就能得到流体通过整个截面的流量，所以写法就是：$\Phi = \iint\limits_S {{\mathbf{v}} \cdot d{\mathbf{S}}}\\$

到此，关于流体的流量就给你点到为止了。麦克斯韦发现流体流量的概念完全可以迁移到电磁学领域里，也就是说把速度𝑣这个向量场换成电场或者磁场这两个向量场，上述结果依然有着极其重要的地位与价值！你在下篇文章里就能看到它的价值，这里首先给它改个名字——向量场的通量。

通量就这样合情合理地出现在你面前了，你会发现根据向量数量积的计算规则，其结果有正负之分。这取决于流速方向与截面法向的夹角𝜃，当夹角在0≤𝜃<90∘范围取值时，通量结果为正；当夹角在90∘<𝜃≤180∘范围内取值时，通量结果为负。

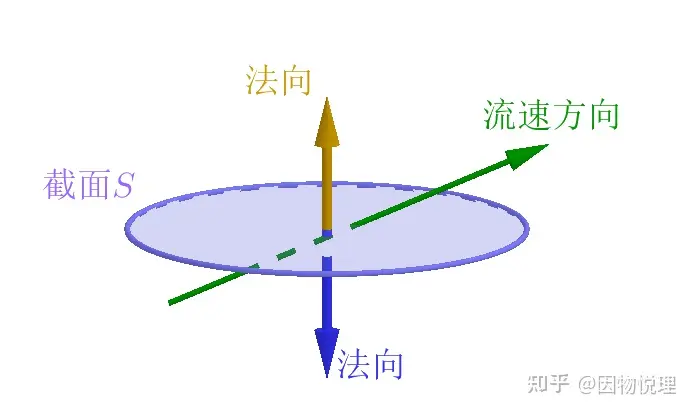
截面的法向可以任选其中一个

从图中可以看到截面的法向是人为二选一的结果，所以通量结果的正负必须与截面的法向对应才行。不过对于闭合曲面来说，大家选择其法向的方式就达成了共识：由截面里面指向外面为截面的法向！

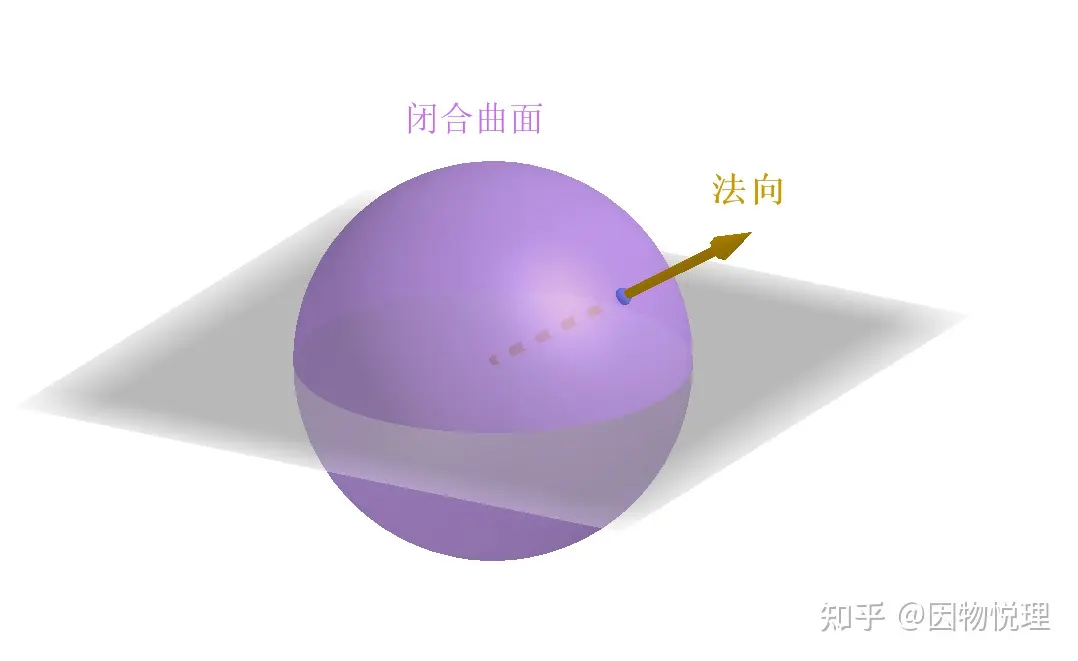
闭合曲面的法向统一选择为由里向外的方向

在这个统一的规定之下，向量场穿过某个闭合曲面的通量$Φ$的正负情况就有了很直观的意义：如果向量场的方向也是从闭合曲面的里面指向外面的，相当于闭合曲面里面有向量场的“源头”，则向量方向与截面法向的夹角必然在0≤𝜃<90∘范围取值，于是通量的结果为正；

反之，向量场的方向由闭合曲面的外面指向其内部，相当于闭合曲面里面有接纳向量场的“漏洞”，则向量方向与截面法向的夹角必然在90∘<𝜃≤180∘范围内取值，故通量的结果为负。

由于正负通量可以相互抵消，对于一个闭合曲面来说，向量场穿过它的通量Φ的取值有三种可能：

（1）$Φ>0$表示流出量大于流入量，说明闭合曲面里面一定有“源”。通俗地说就是该区域里有个水龙头不断在放水，这样才可能有水流出来撒。

（2）$Φ<0$表示流入量大于流出量，说明封闭合面里面有“洞”。通俗地说就是该区域里有坑可以存水，这样才能有水流进来撒。

（3）$Φ=0$表示流出量等于流入量，这就好比一个月光族的现状；当然也有可能是本来就没有流体经过这个区域。

对啦，向量场穿过某个闭合曲面的通量被写为

$\Phi = \mathop{{\oiint}}\limits_S {{\mathbf{v}} \cdot d{\mathbf{S}}} \\$

积分号∯表示咱们是对闭合曲面求通量，所以画个圈，很形象吧？！

相比知道某个闭合区域里是否有“源”或“洞”，咱们也很想知道“源”或“洞”位于哪个点，即咱们也很关心向量场里每个位置的情况。

这就好比用导航，你肯定希望既看到一个区域的大概信息（比如附近有没有堵车和修路）又想得知某个地点的精确信息（能够准确到达目的地）。所以咱们还得为单个点量身定制一个物理量。

容易想到的办法是把包含这个点的闭合曲面𝑆不断缩小，直到极限情形下闭合曲面缩为一个点！不过这种极限情形下，向量场穿个该闭合曲面的通量Φ的极限值必然为零。毕竟你都将面缩为点了，还哪来的面积可言咧？

所以直接用$Φ$的极限值来描绘点的特征不可取。不过考虑到闭合曲面缩小的同时，它所包围的封闭区域的体积$𝑉_𝑆$也是在缩小的，其极限值也为零，咱们就用极限情形下的比值$\frac{Φ}{𝑉_𝑆}$（分子与分母的极限均为零的情形里，比值的极限是可以存在的，参考上篇文章里的例子）来描绘向量场里点的特征。

这个比值的极限便是千呼万唤始出来的向量场的散度！如果向量场依旧用𝑣表示，将向量场中某点$𝑃$处的散度记为${\mathop{\rm div}\nolimits} {\bf{v}}$，则有

${\mathop{\rm div}\nolimits} {\bf{v}} = \mathop {\lim }\limits_{S \to P} \frac{\Phi }{{{V_S}}} = \mathop {\lim }\limits_{S \to P} \frac{1}{{{V_S}}}\mathop{\oiint}\limits_S {{\bf{v}} \cdot d{\bf{S}}} \\$

你看到这里是不是便觉得散度就该这么水到渠成的定义了呢？

从定义可以看出，散度是一个标量，表示在向量场中一点处通量对体积的变化率，也就是该点处对一个单位体积来说所穿过的通量，此即为该点处源的强度。

另外，散度的正负取决于通量的正负，所以散度的结果不仅能体现出该处是源还是洞，还能体现出源（洞）的强度！

搞定了散度，它的定义式里那么一长串的结果怎么就和“$∇$算子”产生了联系呢？

这其实和散度在坐标系里的表示方法有关。散度的定义式里压根就没提坐标系，不过鉴于咱们在很多场合都会用到直角坐标系，所以便有了在直角坐标系里写出散度表示式的需求。

请放心，我可不想写成数学教材那样，所以此处只在直角坐标系里取一个特殊的闭合曲面——立方体表面来简化推导。前方低能预警，有一些公式推导要出现了。

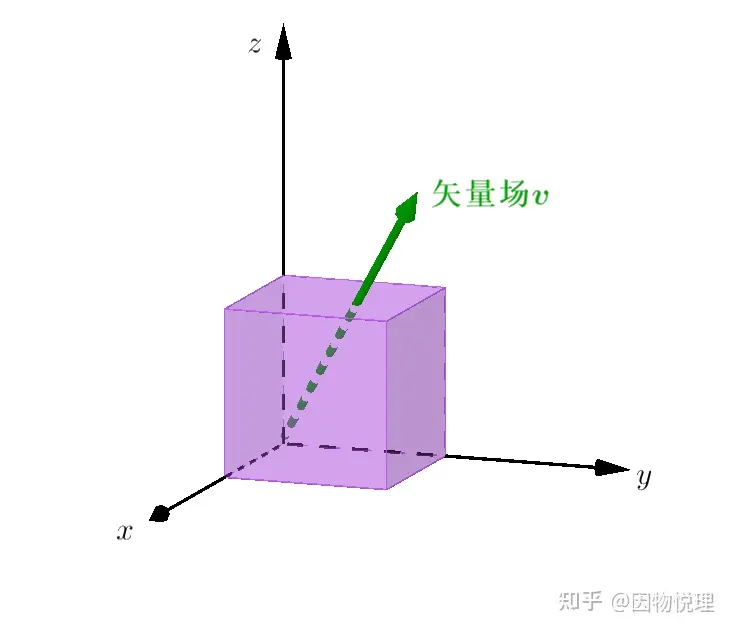
立方体的表面

从示意图里可以看到，向量场$\bf{𝑣}$对这六个表面都会产生通量。不过咱们可以把$𝑣$沿坐标轴𝑥,𝑦,𝑧分解而得到分量$𝑣𝑥,𝑣𝑦,𝑣𝑧$，显然分量𝑣𝑥只对图中的前后两个表面有通量。至于另外两个分量分别对哪些表面有通量就留给你自己找找哈。

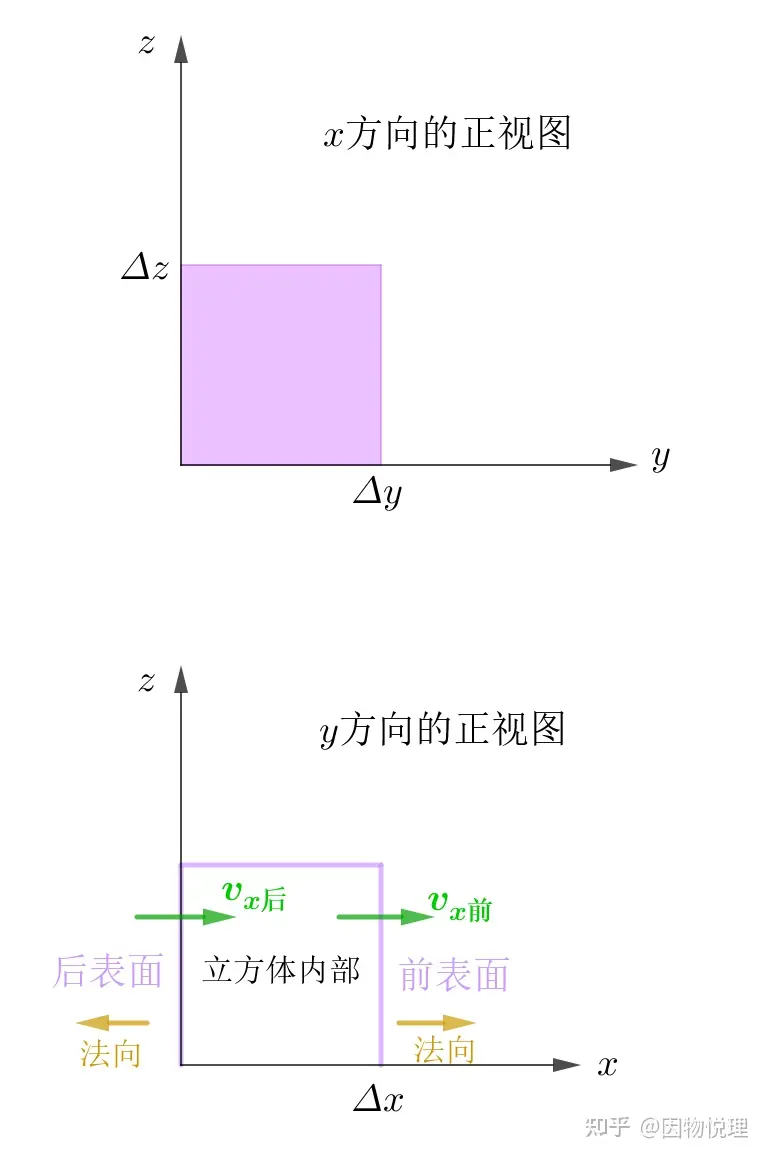
侧视图及其记号

于是咱们可以得到前表面的通量为${\Phi _{前}} = {v_{x(前)} }\times \Delta y \times \Delta z\\$

后表面的通量为${\Phi _{后}} = - {v_x}(后) \times \Delta y \times \Delta z\\$

所以向量场𝑣通过前后两个表面的总通量为前后前后

$Φ1=Φ前+Φ后=[𝑣𝑥(前)−𝑣𝑥(后)]×Δ𝑦×Δ𝑧$

同理，向量场𝑣通过左右两面的总通量为

${\Phi _2} = {\Phi _{左}} + {\Phi _{右}} = [{v_y}(右) - {v_y}(左)] \times \Delta x \times \Delta z\\$

而向量场𝑣通过上下两面的总通量为

${\Phi _3} = {\Phi _{上}} + {\Phi _{下}} = [{v_z}(上) - {v_z}(下)] \times \Delta x \times \Delta y\\$

请自行验证！

式子确实长了一点，但是还算可以看懂不是？继续干！于是向量场𝑣通过这个闭合曲面的总通量为

$\Phi = \mathop{{\oiint}}\limits_S {{\bf{v}} \cdot d{\bf{S}}} = {\Phi _1} + {\Phi _2} + {\Phi _3}\\$

按照散度的定义，向量场𝑣的散度为

$div\bf{v} = \lim\limits_{S \to P} \frac{\Phi }{V_S} =\lim \limits_{S \to P} \frac{{\Phi _1} + {\Phi _2} + {\Phi _3}}{V_S}$

该闭合曲面包裹的空间是个立方体，其体积为

$𝑉𝑆=Δ𝑥×Δ𝑦×Δ𝑧$

当$𝑆→𝑃$时就是要求$Δ𝑥→0,Δ𝑦→0,Δ𝑧→0$

把$𝑉_𝑆$的表达式带入到散度的计算式里，你就会发现很有规律的事情了。

咱们只看第一项$\frac{{{\Phi _1}}}{{{V_s}}}$，化简的结果为$\frac{{{v_x}(前) - {v_x}(后)}}{{\Delta x}}\\$

此结果在$Δ𝑥→0$时的极限值不就是$𝑣_𝑥$对𝑥的偏导数$\frac{{\partial {v_x}}}{{\partial x}}$么？

因为$𝑣_𝑥$在前后两面取不同值是仅由$Δ𝑥$所引起的！如果写成你熟悉的模式，那便是前后${v_x}(前) - {v_x}(后) = {v_x}(x + \Delta x,y,z) - {v_x}(x,y,z)\\$

现在你再去看第一项$\frac{{{\Phi _1}}}{{{V_s}}}$的极限值是不是就清晰明了啦？至于剩下的两项就不用劳烦我亲自动手了吧？

显然第二项$\frac{{{\Phi _2}}}{{{V_s}}}$的极限值为$\frac{{\partial {v_y}}}{{\partial y}}$，第三项$\frac{{{\Phi _3}}}{{{V_s}}}$的极限值为$\frac{{\partial {v_z}}}{{\partial y}}$。

你瞧，咱们轻轻松松地就在直角坐标系里把向量场𝑣的散度给算出来了，结果是d

${\mathop{\rm div}\nolimits} {\bf{v}} = \frac{{\partial {v_x}}}{{\partial x}} + \frac{{\partial {v_y}}}{{\partial y}} + \frac{{\partial {v_z}}}{{\partial z}}\\$

嘿，你还好吗？微积分的计算也不难，对吧？

送你一颗定心丸——上面这个结果虽然是用立方体表面计算出来的，即使换成一般的闭合曲面也是同样的结果，烦请各位自己翻看数学教材里的证明吧。

写到此，在直角坐标系里散度与“$∇$算子”的关系也就浮出水面啦。你看嘛，向量场𝑣在直角坐标系里不是可以写成${\bf{v}} = {v_x}{\bf{i}} + {v_y}{\bf{j}} + {v_z}{\bf{k}}\\$么？

现在只需把“∇算子”$\nabla = \bf{i}\frac{\partial}{\partial x} + \bf{j}\frac{\partial}{\partial y} + \bf{k}\frac{\partial}{\partial z}$和向量场𝑣按向量内积的规则做运算不就有

$\nabla = {\bf{i}}\frac{\partial }{{\partial x}} + {\bf{j}}\frac{\partial }{{\partial y}} + {\bf{k}}\frac{\partial }{{\partial z}}\\$

么？

我一直很讨厌不做任何铺垫就甩出一个定义或者等式，我第一眼看见∇⋅𝑣被定义为散度时也是一脸懵逼！它是谁？从哪来？要到哪里去？一问三不知之后，只剩下心里万马奔腾！不知看到这里的你是否对散度有了清晰地认识呢？

现在咱们回头望一望通量和散度，你会发现通量是定义在曲面上的概念，而散度是定义在点上的概念。它俩都能反映出“源”或“洞”的特征，不过通量是采用了宏观视角而散度却是微观视角。不难想象这两种视角之间应该存在着某种联系。请接好，一个重要的结论即将朝你飞来！

情景很简单，假设一个闭合曲面里面有很多“水龙头”，那么从所有“水龙头”里流出的总流量就等于从整个闭合曲面流出的流量。这意味着咱们在求通量的时候有两种思路。

思路一就是直接从通量的定义出发，写出向量场通过闭合曲面的通量为

$\Phi = \mathop{{\oiint}}\limits_S {{\bf{v}} \cdot d{\bf{S}}} \\$

思路二就是从源头去求通量，也就是从散度的角度求通量。这很简单呀，把封闭区间里所有源头流出的通量求和不就行了么？所以有$\Phi {\text{ = }}\iiint\limits_V {(\nabla \cdot {\mathbf{v}})dV}\\$

如此一来，大名鼎鼎的高斯定理就诞生啦！即

$\iiint\limits_V {(\nabla \cdot {\mathbf{v}})dV} = \mathop{{\oiint}}\limits_S {{\mathbf{v}} \cdot d{\mathbf{S}}} \\$

此乃连接通量和散度的一大利器，你在后续的物理文章里定会遇见它！

向量场的旋度

现在咱们要了解描述流体的另一个重要物理量：环流。不过鉴于环流这个词不好理解，先给你看看与之类似的东东。

你回想一下高中物理里面所讲的圆周运动，物体所受的合力沿圆心方向的分力（即向心力）只能改变物体的运动方向，只有合力沿圆轨迹的切向分力才会使得物体运动得越来快（慢）！

如果你开启物理思维模式，你就会发现这个场景里存在合力对物体做功，所以物体的速度大小才会发生变化。

从下图可以明显看出，在物体沿闭合圆轨迹运动的过程中只有合力的切向分力在做功。按照微积分的做法，在一极小过程中，合力做功为$dW = {F_t}dl\\$

由图中合力方向与切向的关系，合力的功又可以写为。$dW = {\bf{F}} \cdot d{\bf{l}}$

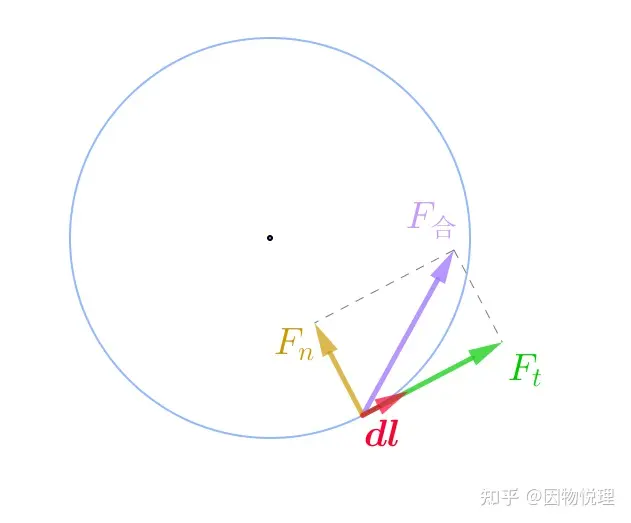
做圆周运动的物体的合力示意图

于是物体沿闭合轨迹𝐿运动一圈后，合力做的总功即为

$𝑊=\oint\limits_S{𝐹⋅𝑑𝑙}$

积分号∮表示对闭合曲线积分，所以很形象地画个圈。此处力沿闭合有向曲线所做的功其实就是环量——顾名思义，环绕某条曲线的量。

再来看流体的环流。在流体流过的某些区域里出现漩涡是一种很常见的现象，如果你在这个漩涡处放一片树叶，它便会随着漩涡而发生旋转。如果你想知道树叶旋转得有多厉害，你可以考虑一下流体速度在树叶的闭合轨迹上有多大的贡献。

因为流速垂直于闭合轨迹方向的分量对树叶的旋转毫无卵用嘛！这与上面做功的例子及其相似，所以咱们也可以照葫芦画瓢地写出积分式

$∮\limits_L𝑣⋅𝑑𝑙$

这便是流体流速沿闭合有向曲线的环流。

如果你非要知道环流有啥物理意义，你可以设想该流体在单位长度上的密度恒为1，则环流就是单位时间里流体沿闭合曲线上的质量。

不仅这两个例子里出现了类似环流的式子，麦克斯韦在电磁场里也发现了类似的积分式子（下篇文章即将出现）。

看来向量场沿着某条闭合曲线的积分好像还是个有头有脸的人物咧！于是数学家表示要剥离其物理背景，让其抽象成一个数学定义：假如向量场依旧用𝑣表示，沿向量场中某条闭合有向曲线𝐿的积分

$Γ=∮\limits_𝐶𝑣⋅𝑑𝑙$

即为向量场沿闭合有向曲线$𝐿$的环量。

说完了环量，你应该知道我马上要说旋度了。和通量与散度的关系类似，如果咱们要关心向量场中某点$𝑃$处的“涡旋”特征时，环量肯定是不行的。原因和前面定义散度一样：咱们需要把包围该点的闭合曲线不断缩向该点，极限情形下所得的环量必然为零（闭合曲线都缩为点了，何来长度咧？）。

考虑到闭合曲线所围区域的面积$𝑆_𝐿$也在不断缩小，其极限值也为零，所以咱们就考虑用环量$Γ$与面积$𝑆_L$的比值的极限值

$\lim\limits_{𝐿⁡\to P}\frac{1}{𝑆_𝐿}∮\limits_𝐿𝑣⋅𝑑𝑙$

去刻画向量场中𝑃点的“涡旋”特征。你若看过了前面关于散度的文字，想必对于这里的操作也就毫不陌生了。

从这个极限值可以看到，它就是环量对面积的变化率，也可以称为环量面密度，反映出向量场中某点的环量强度。

不过与散度不同，它还不是咱们要找的旋度！原因是包含某点的闭合曲线可以有无数条，这里说的无数是指闭合曲线所围区域的法向可以有任意的指向，下图给你明确地展示了出来。

环绕同一点的不同闭合曲线及其法向

而闭合曲线的方向与其法向的关系则由右手螺旋定则来确定，如下图所示。

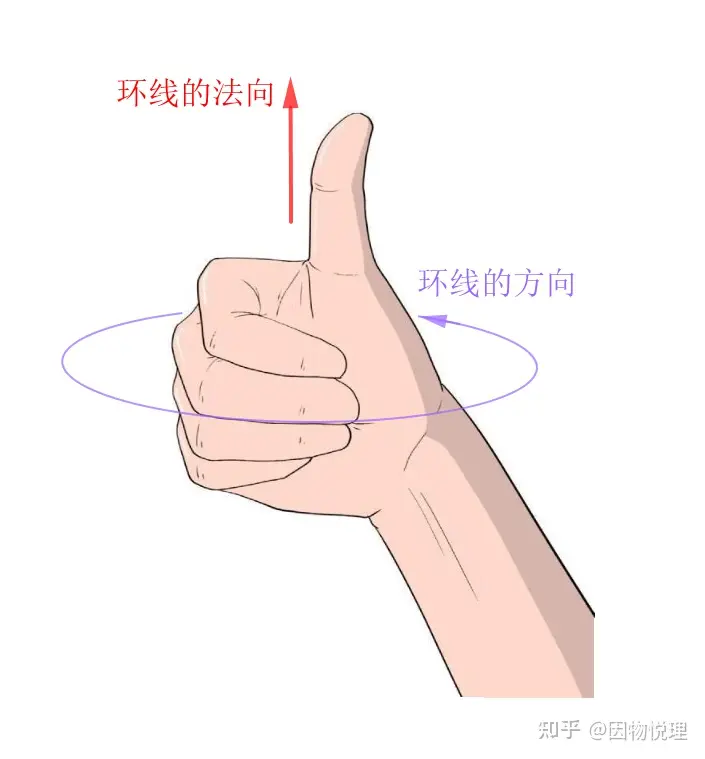
闭合曲线的方向与其法向的关系

也就是说咱们在聊向量场在某点的环量面密度时要指明所沿的方向（即闭合曲线的法向）！

严格的数学证明会告诉你：在所有方向中，有唯一一个方向使得对应的环量面密度取得最大值！可想而知，这么重要的方向岂能逃过咱们的手心？

咱们定义的环量面密度确实可以反映向量场中某点处的环量强度，但是环量面密度是要指明方向的。对于同一个点来说，咱们可以得到无数个方向所对应的环量面密度，它们都能反映出该点的环量强度。

如此一来，问题就出现了——你听谁的？所以咱们一合计，决定听那个最特别的方向以及所对应的环量面密度的话！

于是咱们弄来一个向量$𝑅$，使得它的方向就是这个唯一的方向，且它的大小就是最大的环量面密度，这个向量$𝑅$便很荣幸地被称为向量场𝑣在某点$𝑃$处的旋度，记作$𝑟𝑜𝑡\bf{𝑣}$。

按照定义，旋度为

$𝑟𝑜𝑡𝑣=𝑛_0\lim\limits_{𝐿→𝑃⁡}\frac{1}{𝑆_𝐿}\oint\limits_𝐿𝑣⋅𝑑𝑙$

式子里的$𝑛_0$即为最大环量面密度所对应的那个唯一方向。请注意旋度的向量性以及方向的唯一性！

拿捏住了旋度，你现在应该迫不及待地想知道旋度和“∇算子”之间的关系了吧？和散度的定义一样，旋度的定义也和坐标系毫无关系，咱们现在要做的就是写出旋度在直角坐标系里的表示式。

关于旋度向量有一个重要的性质：它沿某个方向上的分量等于该方向上的环量面密度。这纯粹是一个数学结论，烦请你翻阅一下数学教材吧。

放在直角坐标系来说，某点的旋度向量$𝑅$可以沿三个坐标方向进行分解，即有

$𝑅=𝑅_𝑥𝑖+𝑅_𝑦𝑗+𝑅_𝑧𝑘$则分量𝑅𝑥的值便等于该点处沿𝑖轴方向的环量面密度，分量𝑅𝑦的值便等于该点处沿𝑗轴方向的环量面密度，分量𝑅𝑧的值便等于该点处沿𝑘轴方向的环量面密度。

了解这个重要性质后就可以开始数学推演啦，前方有公式低能预警！

咱们选向量场中的$𝑃$点为考察对象，为了方便，待会我将用特殊形状的闭合曲线来围住它。现在先拿分量$𝑅𝑥$来试试手，所以咱们要计算$𝑃$点处沿$𝑖$轴方向的环量面密度。

显然以$𝑖$轴为法向的平面是一系列与$𝑗𝑜𝑘$平面平行的平面，在这些平面里包含$𝑃$点的只有一个，于是咱们就在这个平面里画一条闭合曲线围住$𝑃$点，并且毫不犹豫地选择了矩形闭合曲线。无他，就是因为用起来方便。

对了，计算环量的时候不得考虑闭合曲线的方向么？这里有个统一的规定：按照右手螺旋定则来确定——即右手四指绕行的方向为封闭曲线的方向、大拇指的指向为封闭曲线所围区域的法向。

另外把向量场$𝑣$也沿三个坐标轴进行分解，分别记为$𝑣𝑥$、$𝑣𝑦$和$𝑣𝑧$。

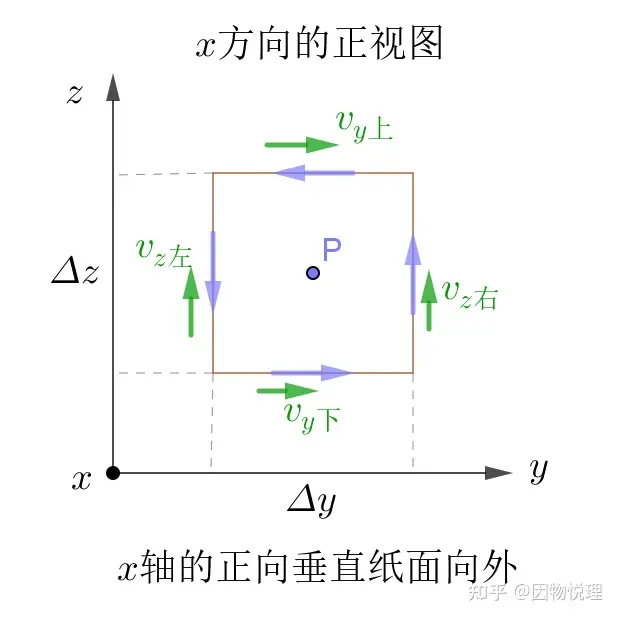
侧视图：闭合曲线的方向与向量场分量的方向

一切准备就绪，向量场𝑣沿上图中这条长宽分别为Δ𝑦与Δ𝑧的闭合矩形线的环量即为

$∮\limits_{𝐿_𝑥}𝑣⋅𝑑𝑙=𝑣_𝑦(下)Δ𝑦−𝑣_𝑦(上)Δ𝑦+𝑣_𝑧(右)Δ𝑧−𝑣_𝑧(左)Δ𝑧$

这个式子看起来应该很容易理解吧？因为只有当向量分量与矩形边平行时才对环量有贡献撒！

然后再把环量除以矩形的面积，显然它的面积为

$𝑆=Δ𝑦×Δ𝑧$

请你自行验证一下，化简的结果为

$\frac{∮\limits_{𝐿_𝑥}𝑣⋅𝑑𝑙}{𝑆}=\frac{𝑣_𝑧(右)−𝑣𝑧(左)}{Δ𝑦}−\frac{𝑣_𝑦(上)−𝑣_𝑦(下)}{Δ𝑧}$

最后对它取极限$𝐿_𝑥→𝑃$，咱们就完成了环量面密度的计算。

要使得$𝐿_𝑥→𝑃$，其实就是要求

$Δ𝑦→0,Δ𝑧→0$

所以你会发现上面化简结果里第一项的极限值为

$\lim\limits_{Δ𝑦→0}\frac{⁡𝑣_𝑧(右)−𝑣_𝑧(左)}{Δ𝑦}=\frac{∂𝑣_𝑧}{∂𝑦}$

为啥？因为分量𝑣𝑧在左右两面取不同值是仅由Δ𝑦所引起的！如果写成你熟悉的模式，那便是

$𝑣_𝑧(右)−𝑣_𝑧(左)=𝑣_𝑧(𝑥,𝑦+Δ𝑦,𝑧)−𝑣_𝑧(𝑥,𝑦,𝑧)$

现在你再去看极限值的结果是不是就很清晰了撒？

同理，上述化简结果里第二项的极限值便是

$\lim\limits_{Δ𝑧→0}\frac{⁡𝑣_𝑦(上)−𝑣_𝑦(下)}{Δ𝑧}=\frac{∂𝑣_𝑦}{∂𝑧}$

于是咱们就得到旋度向量$𝑅$沿$𝑖$轴的分量$𝑅𝑥$的大小，即为

$𝑅𝑥=\frac{∂𝑣_𝑧}{∂𝑦}−\frac{∂𝑣_𝑦}{∂𝑧}$

剩下照葫芦画瓢的工作就不用我亲自动手了吧？留点作业给你哈。

最终可得旋度向量$𝑅$沿$𝑗$轴的分量$𝑅𝑦$的大小为

$𝑅𝑦=\frac{∂𝑣_𝑥}{∂𝑧}−\frac{∂𝑣_𝑧}{∂𝑥}$

旋度向量𝑅沿𝑘轴的分量𝑅𝑧的大小为

$𝑅𝑧=\frac{∂𝑣_𝑦}{∂𝑥}−\frac{∂𝑣_𝑥}{∂𝑦}$

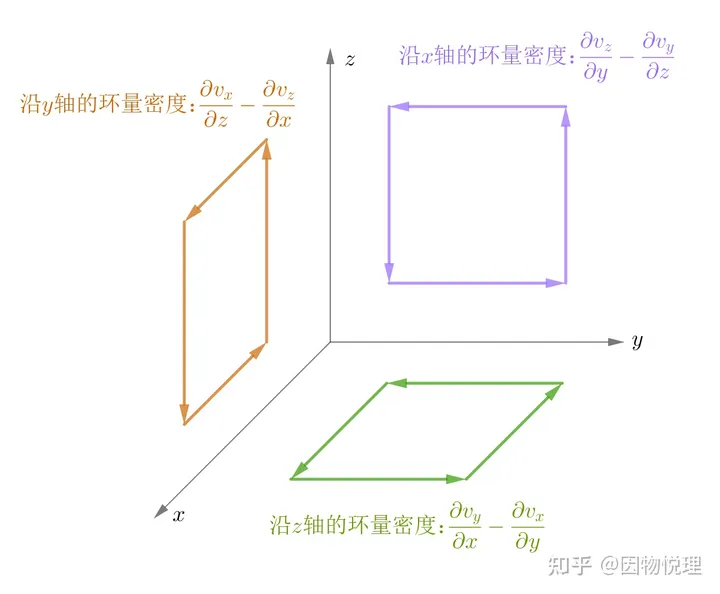
直角坐标系里，旋度向量沿各个方向的分量大小

撒花，在直角坐标系里的旋度表示式出炉啦！即向量场𝑣在某点处的旋度为

$𝑟𝑜𝑡𝑣=(\frac{∂𝑣_𝑧}{∂𝑦}−\frac{∂𝑣_𝑦}{∂𝑧})𝑖+(\frac{∂𝑣_𝑥}{∂𝑧}−\frac{∂𝑣_𝑧}{∂𝑥})𝑗+(\frac{∂𝑣_𝑦}{∂𝑥}−\frac{∂𝑣_𝑥}{∂𝑦})𝑘$

呃，这个结果看起来眼熟不？记不起来了就往前去瞧瞧什么是向量外积，看完你就会发现“$∇$算子”简直就是为这个结果量身定制的记号，即

$𝑟𝑜𝑡𝑣=∇×𝑣$

弱弱地问你一句，上面这个旋度的表示式能准确记住么？我要不写这篇文章，我也记不住。要记住它的方法也很多，我习惯于自己画出下图来帮助记忆。

你发现没，旋度表示式里的每个分量的形式完全相同，都长成

$\frac{∂𝑣×}{∂∗}−\frac{∂𝑣∗}{∂×}$

这般模样，唯一的区别在于‘×’和‘∗’分别代表哪个分量坐标。

从这个图里可以看到，当咱们要写𝑖分量（也就是𝑥分量）时，你先把图中的𝑥划掉，于是‘×’和‘∗’只能在𝑦和𝑧中选。

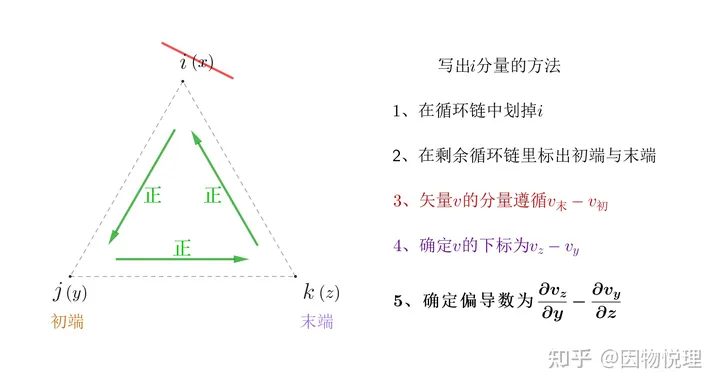
记忆旋度表达式的“三角形”

由于划掉了𝑥，则𝑧处于循环链的末端，于是规律就变成了用处于循环链末端的字母构成的向量分量‘减’用初端的字母构成的向量分量！之所以‘减’加上引号，上图里解释得很清楚。

不知你现在看到∇×𝑣后还会不会茫然到怀疑人生呢？如果上面的文字有幸能让你对旋度有了清晰的认知，那就赶紧加个鸡腿给自己犒劳一下吧！慢慢吃，品尝美食之后还要向你介绍一个重要结论呢！

类似于通量和散度通过高斯公式这座桥梁取得了联系，环量和旋度之间也有着密不可分的关系。

想要得知向量场𝑣沿闭合曲线𝐿的环量可以直接求出$∮\limits_𝐿𝑣⋅𝑑𝑙$的结果。

而从另一个角度来看，假设有一个以这条闭合曲线为边界的曲面，把它分割成很多个矩形网格，显然所有网格的环量和就是这个曲面边界即闭合曲线上的环量。

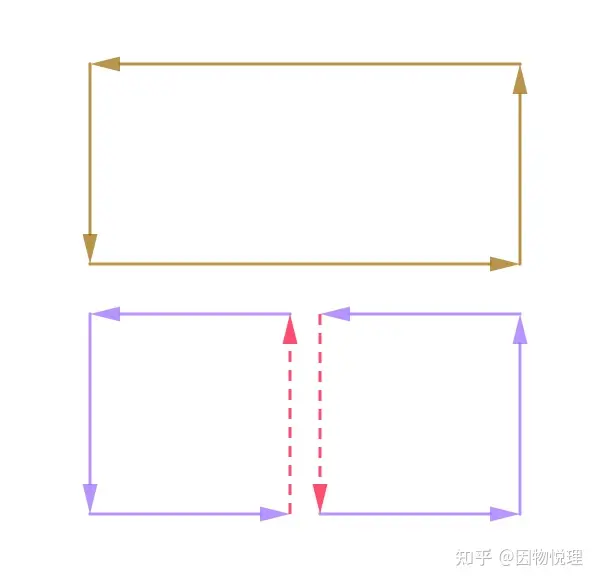
两个内部小环量形成一个边界大环量

至于小网格里的环量是多少，根据环量面密度的定义，咱们可以立刻得出环量面密度乘以小网格的面积等于小网格的环量（需要在小网格面积趋于零的情形下）。

前面告知过你旋度的一个重要特性：旋度沿某个方向上的分量等于该方向上的环量面密度。

利用这个特性，刚才用文字描述的乘法便可写成

$(∇×𝑣)⋅𝑑𝑆$

至于你要求得所有网格里的环量，是不是得把积分用起来？于是便有了积分式

$\iint\limits_𝑆(∇×𝑣)⋅𝑑𝑆$

严格的证明过程请自觉查询数学教材哈！

从两种途径均能得到向量场𝑣沿闭合曲线𝐿的环量，所以有

$\iint\limits_s(∇×𝑣)⋅𝑑𝑆=∮\limits_𝐿𝑣⋅𝑑𝐿$这便是如雷贯耳的斯托克斯公式。

需要说明的是，同一条闭合曲线𝐿可以对应着无数个以它为边界的曲面。你想象一下吹泡泡的圆圈，不管泡泡被吹得多大，泡泡们都是以这个圆圈为边界！但斯托克斯公式表示它不挑曲面，只要闭合曲线𝐿定了，不管以它为边界的曲面是啥样，积分式的结果都等于$\oint\limits_𝐿𝑣⋅𝑑𝑙$

无论泡泡吹得有多大，泡泡的边界始终都是这个红色的圈

敲黑板，后续的物理文章里会出现斯托克斯公式的身影，别忘了它！

标量场的梯度

呃，你是不是搞错了啊？整篇文章都在围绕向量展开，你这里说标量干啥？其实我也不打算让标量搅局，奈何人家的梯度是向量啊！这是怎么回事？请耐心往下看。

什么是标量场我就不重复唠叨了，前面在说向量场时已经顺带介绍过。为了具体知道标量场区域里每处的值，咱们可以把每个点的数值写出来。可想而知的是这个区域会被无数个数值给覆盖，这和给向量场里的每点标出有向箭头一样吃力不讨好，所以还是不要这么干。

参考力线或者流线可以简洁清晰地描绘向量场，咱们完全可以借鉴嘛——把标量场中数值相同的点连成曲线！这样的曲线称为等值线。顾名思义，同一条等值线上所有点的取值都一样，所以咱们只需给每条等值线标出一个数值即可。

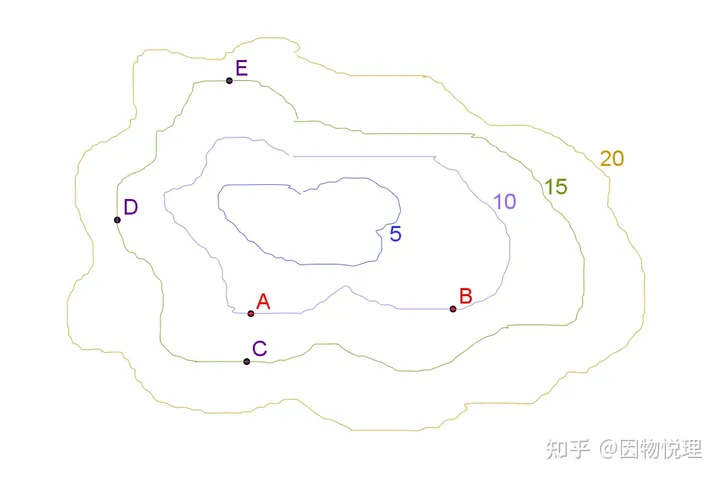
等值线的示意图

有了等值线就能帮助咱们判断标量场随位置变化的特点啦。你看上图，𝐴、𝐵两点的值相同而𝐴的值小于𝐶的值；然而你也会发现𝐴的值比𝐶、𝐷、𝐸的值小得一样多，但是却有明显的区别——毕竟𝐴点到这三点的距离不一样嘛。

为了有工具来描述这个差异，咱们需要引进等值线的法向。为了方便，咱们现在把等值线画成直线（对于曲线来说，你取一小段不也可近似看成直线么？反正咱们现在是着眼于线上的某点），然后画出它的法向，规定其方向由高等值线指向低等值线。

你是不是好奇为什么偏偏选中了等值线的法向呢？

你看嘛，沿垂直法向方向，标量场的值肯定不变；而沿着法向方向，标量场变化相同的值所需的距离最短，即标量场沿法向变化得最快！这一下就把标量场随位置变化的特征全给抓住了，试问还有哪个方向能与之一战？

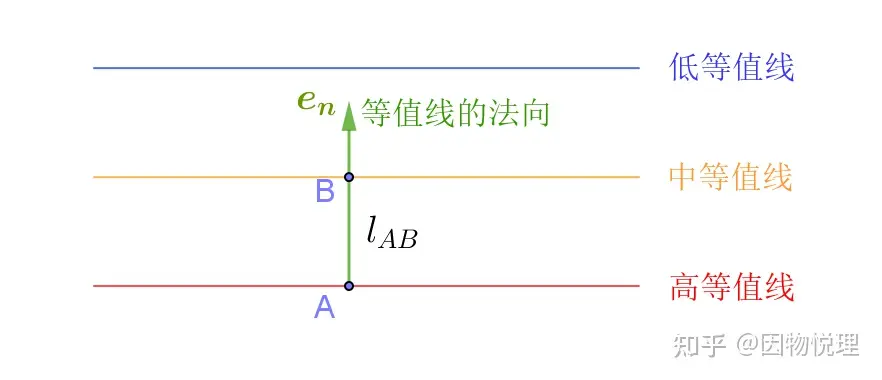
等值线与其法向的关系

钦定了法向，标量场𝑓沿此方向随距离的变化率就显得尤为重要啦！因为它直接反映出沿等值线法向单位距离上标量场变化的大小！通过这段文字描述，你应该能写出这个变化率的表达式吧？

按上图里所标的字母，此变化率为

$\frac{𝑓(𝐵)−𝑓(𝐴)}{𝑙_{𝐴𝐵}}$

当然了，咱们不会直接用这个式子，而是用它的极限情形，因为我们关心的是𝐴点处的变化率。所以咱们写出的极限值为

$\lim\limits_{𝐵→𝐴⁡}\frac{𝑓(𝐵)−𝑓(𝐴)}{𝑙_{𝐴𝐵}}$

同时为了强调这个变化率是沿着等值线的法向，所以给这个极限值带上法向方向，将所得的向量就命名为标量场𝑓在𝐴点处的梯度，记作$𝑔𝑟𝑎𝑑\large𝑓$。

现在你应该明白为啥要给你介绍标量场的梯度了吧？人家打从娘胎里出来就是向量！而且它还自带重要属性：标量场中的数值沿着梯度方向变化得最快！

按照定义，标量场𝑓的梯度为$𝑔𝑟𝑎𝑑𝑓=\lim\limits_{𝐵→𝐴}\frac{⁡𝑓(𝐵)−𝑓(𝐴)}{𝑙_{𝐴𝐵}}𝑒_𝑛$

提醒你一下，这个极限值眼熟不？是不是和导数的定义很像？那咱们就把这个极限值写成我们熟悉的导数形式，梯度即为

$𝑔𝑟𝑎𝑑\large𝑓=\frac{∂𝑓}{∂𝑙}𝑒_𝑛$

之所以写成偏导，是因为标量场𝑓除了与位置有关，或许还会随时间以及其他因素变化呢？而梯度定义里面，咱们只关注位置变化所带来的标量场值的变化，所以写成偏导数没毛病。

你看到这里就会发现，梯度也和散度、旋度一样，其定义方式压根就没坐标系啥事。所以接下来要做的就是找出梯度在直角坐标系里的表示式，然后就能发现它和“∇算子”之间的关系啦。

为了方便画图，咱们暂且只考虑平面直角坐标系吧。根据下图中所标出的符号，𝐴、𝐵两点间的标量差就等于𝑓(𝑥+Δ𝑥,𝑦+Δ𝑦)−𝑓(𝑥,𝑦)这不就是上篇文章里所介绍的多元函数的全增量么？

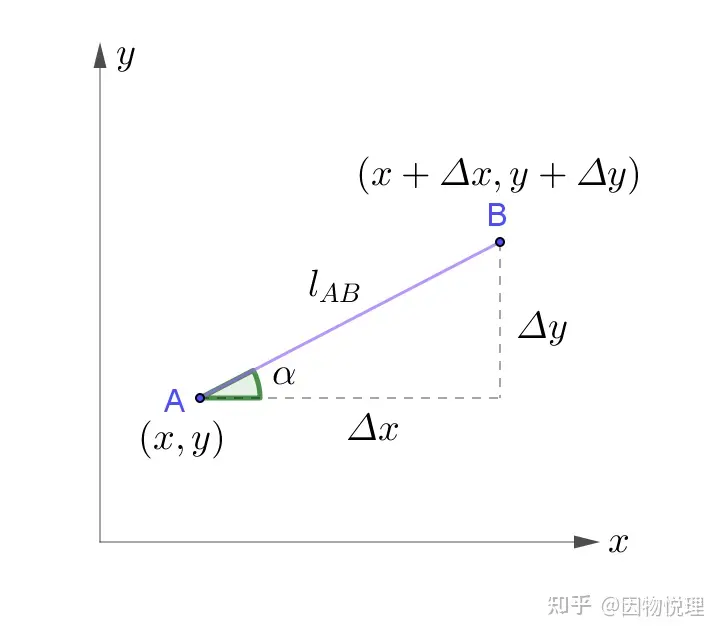
结论

$𝑓(𝑥+Δ𝑥,𝑦+Δ𝑦)−𝑓(𝑥,𝑦)=\frac{∂𝑓}{∂𝑥}Δ𝑥+\frac{∂𝑓}{∂𝑦}Δ𝑦+𝑜(Δ𝑥2+Δ𝑦2)$

直接用起来嘛。

发现没，高阶无穷小量里的

$\sqrt{Δ𝑥2+Δ𝑦2}$

正好是$𝐴、𝐵$两点间的距离$𝑙_{𝐴𝐵}$，所以极限值

$\lim\limits_{𝐵→𝐴}\frac{⁡𝑓(𝐵)−𝑓(𝐴)}{𝑙_{𝐴𝐵}}=\frac{∂𝑓}{∂𝑥}cos⁡\alpha+\frac{∂𝑓}{∂𝑦}sin⁡\alpha$

这是因为

$\lim\limits_{𝐵→𝐴⁡}\frac{\Delta𝑥}{𝑙_{𝐴𝐵}}=cos⁡\alpha$

$\lim\limits_{𝐵→𝐴}\frac{⁡Δ𝑦}{𝑙_{𝐴𝐵}}=sin⁡\alpha$

等式里的𝛼就是图中所标注的夹角。以及

$\lim\limits_{𝐵→𝐴⁡}\Large{\frac{𝑜(𝑙_{𝐴𝐵})}{𝑙_{𝐴𝐵}}}=0$

烦请你再瞄一下上面这个示意图，你会发现由𝐴指向𝐵的单位矢量$𝑒_{𝐴𝐵}$（姑且这么暂记）在该直角坐标系里即可写成

$𝑒_{𝐴𝐵}=𝑖cos⁡\alpha+𝑗sin⁡\alpha$

所以刚才求得的极限结果不就可以写成

$\lim\limits_{𝐵→𝐴}⁡\frac{𝑓(𝐵)−𝑓(𝐴)}{𝑙_{𝐴𝐵}}=(𝑖\frac{∂𝑓}{∂𝑥}+𝑗\frac{∂𝑓}{∂𝑦})⋅(𝑖cos⁡\alpha+𝑗sin⁡\alpha)=(𝑖\frac{∂𝑓}{∂𝑥}+𝑗\frac{∂𝑓}{∂𝑦})⋅𝑒_{𝐴𝐵}$

的向量内积形式了么？

咳咳，请注意啦！咱们在求出这个极限值的时候，虽然咱们心里清楚由𝐴指向𝐵的方向即为函数𝑓在𝐴点处的梯度方向，但是从上面的推导过程来，无论𝐴指向𝐵的方向如何，这个极限结果都能写成上面的形式！如此一来，梯度方向的唯一性怎么体现呢？

还记得梯度方向的特点么？标量场沿梯度方向变化得最快！也就是说标量场沿梯度方向上，极限

$\lim\limits_{𝐵→𝐴}\frac{⁡𝑓(𝐵)−𝑓(𝐴)}{𝑙_{𝐴𝐵}}$有最大值！是时候让这个特点发挥作用啦。

咱们可以这么看，极限结果里的第一个向量$(𝑖\frac{∂𝑓}{∂𝑥}+𝑗\frac{∂𝑓}{∂𝑦})$是个固定向量，我的意思是说在你选定了𝐴点之后，这个向量的结果就是确定的啦。为了方便接下来的描述，姑且把这个固定向量记为𝐺。

于是极限值可以写成

$\lim\limits_{𝐵→𝐴}\frac{⁡𝑓(𝐵)−𝑓(𝐴)}{𝑙_{𝐴𝐵}}=𝐺⋅𝑒_{𝐴𝐵}=|𝐺|cos⁡(𝐺,𝑒_{𝐴𝐵})$

你现在看出什么了没？在向量𝐺为固定向量的前提下，要使得极限

lim𝐵→𝐴⁡𝑓(𝐵)−𝑓(𝐴)𝑙𝐴𝐵有最大值，只能是单位矢量𝑒𝐴𝐵与固定向量𝐺同向时才行！

因为只有这种情况下，$cos⁡(𝐺,𝑒_{𝐴𝐵})$才能取得最大值1。如此一来，极限$\lim\limits_{𝐵→𝐴}\frac{⁡𝑓(𝐵)−𝑓(𝐴)}{𝑙_{𝐴𝐵}}$的最大值即为|𝐺|。

你觉得此时的$𝑒_{𝐴𝐵}$是哪个方向呢？肯定就是标量场的梯度方向撒！

由于此时的$𝑒_𝐴𝐵$与固定向量𝐺同方向，意味着𝐺也与梯度方向相同！

而且固定向量𝐺的长度又是极限$\lim\limits_{𝐵→𝐴}\frac{⁡𝑓(𝐵)−𝑓(𝐴)}{𝑙_{𝐴𝐵}}$的最大值，请问𝐺不是梯度谁是梯度呢？！即𝑔𝑟𝑎𝑑𝑓=𝐺。

于是咱们就找到了梯度在平面直角坐标系里的表示式：

$𝑔𝑟𝑎𝑑\large{𝑓}=i\frac{∂𝑓}{∂𝑥}+𝑗\frac{∂𝑓}{∂𝑦}$

至于标量场存在于空间范围里，咱们就要启用空间直角坐标系。参考上面的推导过程，加一副碗筷的事嘛！即

$𝑔𝑟𝑎𝑑\large{𝑓}=\frac{∂𝑓}{∂𝑥}𝑖+\frac{∂𝑓}{∂𝑦}𝑗+\frac{∂𝑓}{∂𝑧}𝑘$这便是梯度在直角坐标系里的表示式啦。

看到这个结果，你对$𝑔𝑟𝑎𝑑\large𝑓=∇𝑓$还有啥疑问吗？

结语

这篇关于向量的介绍主要是为后续即将到来的物理内容服务，所以仅仅涉及向量的一些皮毛知识，部分结论只是浅尝辄止。

不过我依旧按照个人的行文风格将向量概念及其性质的来龙去脉尽量说明白，以此希望你看完后能在头脑里形成一条关于向量的完整逻辑线。

不知看到这里的你是否已经解决了前言里抛出的两个疑问呢？相比知其然，知其所以然是不是更有意思呢？比起教科书上冷冰冰的定义，向量背后的故事是否让你对它有了更深刻的印象呢？如果能有此效果，我深感欣慰！